题目内容
18.已知f(x)=$\frac{1}{x(x+1)}$,则f(1)=$\frac{1}{1×(1+1)}$=$\frac{1}{1×2}$,f(2)=$\frac{1}{2×(2+1)}$=$\frac{1}{2×3}$…,则:(1)f(3)=$\frac{1}{12}$;
(2)f(1)+f(2)+f(3)=$\frac{3}{4}$;
(3)化简:f(1)+f(2)+f(3)+…+f(n).
分析 (1)将x=3代入进行计算即可;
(2)f(1)=$\frac{1}{2}=1-\frac{1}{2}$;f(2)=$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$;f(3)=$\frac{1}{3}-\frac{1}{4}$;
(3)利用(2)中的规律进行计算即可.
解答 解:(1)f(3)=$\frac{1}{3×(3+1)}=\frac{1}{3×4}=\frac{1}{12}$
故答案为:$\frac{1}{12}$.
(2)f(1)+f(2)+f(3)=$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}$=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$=1$-\frac{1}{4}$=$\frac{3}{4}$;
故答案为:$\frac{3}{4}$.
(3)f(1)+f(2)+f(3)+…+f(n)═$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}$+…+$\frac{1}{n×(n+1)}$=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题主要考查的是有理数的计算,利用拆项裂项法进行简便运算是解题的关键.

练习册系列答案
相关题目
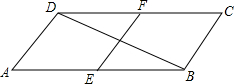 已知:如图,在?ABCD中,∠A=60°,E、F分别为AB、CD的中点,AB=2AD,BD=4$\sqrt{3}$,求EF的长.
已知:如图,在?ABCD中,∠A=60°,E、F分别为AB、CD的中点,AB=2AD,BD=4$\sqrt{3}$,求EF的长. 已知线段a(如图),把它分成1:2:3三段.
已知线段a(如图),把它分成1:2:3三段.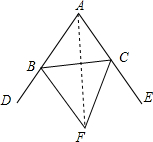 如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证:
如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证: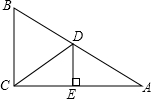 已知:如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AC的垂直平分线与AB交于点D,E为垂足,DE=2cm,求△BCD的周长.
已知:如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AC的垂直平分线与AB交于点D,E为垂足,DE=2cm,求△BCD的周长. 如图,在?ABCD中,AC=4cm,BD=6cm,对角线AC、BD相交于点O,AC⊥AB,求?ABCD的周长.
如图,在?ABCD中,AC=4cm,BD=6cm,对角线AC、BD相交于点O,AC⊥AB,求?ABCD的周长.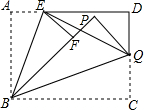 如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把∠A沿BE折叠,使点A落在F处,点Q是CD上一点,将∠C沿BQ折叠,点C恰好落在直线BF上,若∠BQE=45°,则AE=2.
如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把∠A沿BE折叠,使点A落在F处,点Q是CD上一点,将∠C沿BQ折叠,点C恰好落在直线BF上,若∠BQE=45°,则AE=2.