题目内容
3.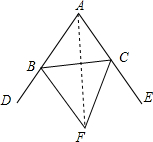 如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证:
如图,△ABC的外角∠CBD,∠BCE的平分线相交于点F,求证:(1)∠BFC=90°-$\frac{1}{2}$∠BAC;
(2)点F在∠DAE的平分线上.
分析 (1)根据三角形内角和定理和角平分线的定义计算即可;
(2)作FG⊥AB于G,FH⊥BC于H,FQ⊥AC于Q,根据角平分线的性质定理和判定定理证明即可.
解答 证明:(1)∵∠ABC+∠ACB=180°-∠BAC,
∴∠DBC+∠ECB=180°+∠BAC,
∵BF、CF是∠CBD,∠BCE的平分线,
∴∠FBC+∠FCB=$\frac{1}{2}$(∠DBC+∠ECB)=90°+$\frac{1}{2}$∠BAC,
∴∠BFC=180°-(∠FBC+∠FCB)=90°-$\frac{1}{2}$∠BAC;
(2) 作FG⊥AB于G,FH⊥BC于H,FQ⊥AC于Q,
作FG⊥AB于G,FH⊥BC于H,FQ⊥AC于Q,
∵BF、CF是∠CBD,∠BCE的平分线,FG⊥AB,FH⊥BC,FQ⊥AC,
∴FG=FH,FE=FH,
∴FG=FE,又FG⊥AB,FQ⊥AC,
∴F在∠DAE的平分线上.
点评 本题考查的是角平分线的性质和判定以及三角形内角和定理,掌握角的平分线上的点到角的两边的距离相等、到角的两边的距离相等的点在角的平分线上是解题的关键.

练习册系列答案
相关题目
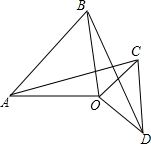 如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°,当将△COD绕点O顺时针旋转时,连线AC与BD之间的大小关系如何?试猜想并证明你的结论.
如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°,当将△COD绕点O顺时针旋转时,连线AC与BD之间的大小关系如何?试猜想并证明你的结论. 如图,正方形ABCD与正方形EFGH分别是同一个圆的外切四边形与内接四边形,四边形ABCD与正方形EFGH的面积之比是2:1.
如图,正方形ABCD与正方形EFGH分别是同一个圆的外切四边形与内接四边形,四边形ABCD与正方形EFGH的面积之比是2:1.