题目内容
9. 如图,在?ABCD中,AC=4cm,BD=6cm,对角线AC、BD相交于点O,AC⊥AB,求?ABCD的周长.
如图,在?ABCD中,AC=4cm,BD=6cm,对角线AC、BD相交于点O,AC⊥AB,求?ABCD的周长.
分析 由平行四边形的性质得出AB=CD,AD=BC,OA=$\frac{1}{2}$AC=2cm,OB=$\frac{1}{2}$BD=3cm,由勾股定理求出AB,再由勾股定理求出BC,即可得出四边形ABCD的周长.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=$\frac{1}{2}$AC=2cm,OB=$\frac{1}{2}$BD=3cm,
∵AC⊥AB,
∴∠BAO=90°,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$(cm),
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{(\sqrt{5})^{2}+{4}^{2}}$=$\sqrt{21}$,
∴?ABCD的周长=2(AB+BC)=2($\sqrt{5}$+$\sqrt{21}$)=2$\sqrt{5}$+2$\sqrt{21}$(cm).
点评 本题考查了平行四边形的性质、勾股定理、平行四边形周长的计算;熟练掌握平行四边形的性质和勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
17.已知点A、B,且AB>4,画经过A、B两点且半径为2的圆有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
 如图,正方形ABCD与正方形EFGH分别是同一个圆的外切四边形与内接四边形,四边形ABCD与正方形EFGH的面积之比是2:1.
如图,正方形ABCD与正方形EFGH分别是同一个圆的外切四边形与内接四边形,四边形ABCD与正方形EFGH的面积之比是2:1.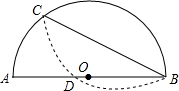 如图,BC为半圆中一条非直径的弦,现将$\widehat{BC}$沿弦BC对对折后交直径AB于点D,若AB=10,CB=4$\sqrt{5}$,则$\frac{AD}{DB}$的值为$\frac{2}{3}$.
如图,BC为半圆中一条非直径的弦,现将$\widehat{BC}$沿弦BC对对折后交直径AB于点D,若AB=10,CB=4$\sqrt{5}$,则$\frac{AD}{DB}$的值为$\frac{2}{3}$.