题目内容
14.利民水果超市销售一种时令水果,第一周的进价是每千克30元,销量是200千克;第二周的进价是每千克25元,销量是400千克.已知第二周的售价比第一周的售价每千克少10元,第二周比第一周多获利2000元.(1)求第二周该水果每千克的售价是多少元?
(2)第三周该水果的进价是每千克20元.经市场调查发现,如果第三周的售价比第二周降低t%,则销量会比第二周增加 5t%.请写出第三周获利y(元)与t的函数关系式,并求出t为何值时,y最大?最大值是多少?
分析 (1)利用分别表示出两周的利润进而得出等式求出答案;
(2)根据题意表示出第三周的销量与每千克利润,进而得出y与t的函数关系式进而得出答案.
解答 解:(1)第二周该水果每千克售价是x元.
则 400(x-25)=200(x+10-30)+2000,
解得:x=40,
答:第二周该水果每千克售价是40元;
(2)根据题意可得:
y=400(1+5t%)×[40(1-t%)-20],
=(400+20t)(20-0.4t),
=-8t2+240t+8000,
∵-8<0,抛物线开口向下,
∴当t=-$\frac{240}{2×(-8)}$=15时,
y最大=(400+20×15)(20-0.4×15)=9800(元).
点评 此题主要考查了一元一次方程的应用以及二次函数的应用,正确表示出第三周的销量与每千克利润是解题关键.

练习册系列答案
相关题目
6.满足下列条件的三条线段a、b、c能构成三角形的是( )
| A. | a:b:c=1:2:3 | B. | a+b=4,a+b+c=9 | C. | a=3,b=4,c=5 | D. | a:b:c=1:1:2 |
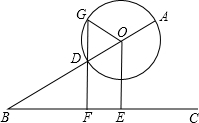 如图,线段AB与射线BC的夹角为30°,点O是AB上一动点,以点O为圆心,OA为半径作⊙O,交线段AB于另一点D,过点O作OE⊥BC于点E,过点D作直线DF⊥BC于点F,交⊙O于另一点G.
如图,线段AB与射线BC的夹角为30°,点O是AB上一动点,以点O为圆心,OA为半径作⊙O,交线段AB于另一点D,过点O作OE⊥BC于点E,过点D作直线DF⊥BC于点F,交⊙O于另一点G. 已知:如图,AB∥CD,∠A=∠D.求证:AF∥ED.
已知:如图,AB∥CD,∠A=∠D.求证:AF∥ED. 已知:如图,△ABC中,DE∥BC,EF∥AB,BE平分∠ABC.
已知:如图,△ABC中,DE∥BC,EF∥AB,BE平分∠ABC.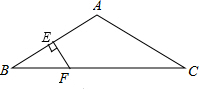 如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF.
如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF. 已知梯形ABCD中,AD∥BC,AB=AD=DC,点E、F分别是对角线AC、BD的中点.求证:四边形ADEF为等腰梯形.
已知梯形ABCD中,AD∥BC,AB=AD=DC,点E、F分别是对角线AC、BD的中点.求证:四边形ADEF为等腰梯形.