Question

4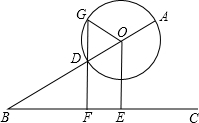．如图，线段AB与射线BC的夹角为30°，点O是AB上一动点，以点O为圆心，OA为半径作⊙O，交线段AB于另一点D，过点O作OE⊥BC于点E，过点D作直线DF⊥BC于点F，交⊙O于另一点G．
（1）探究当点O运动时，点G运动的轨迹是否有规律？请说明理由．
（2）连接DE，探究四边形DEOG是否能够成为菱形？如果可以，请判断点O此时的位置以及⊙O与BC的位置关系，并说明理由．如果不可以，也请解释原因．

Answer 1

分析 （1）连接AG，由直径所对的圆周角为90°可得出AG⊥GD，再结合DF⊥BC利用“垂直于同一直线的两直线平行”即可得出AG∥BC；
（2）连接DE，由（1）的结论即可得出GD=$\frac{1}{2}$AD，再根据菱形的性质即可得出OE=GD=$\frac{1}{2}$AD，进而得出⊙O与BC相切与点E，结合∠ABC=30°，即可得出OA=$\frac{1}{3}$AB．

解答 解：（1）如图1，连接AG，AG∥BC，理由如下：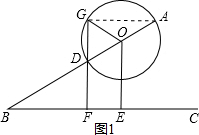
∵AD为⊙O的直径，
∴∠AGD=90°，
∴AG⊥GD，
∵DF⊥BC，
∴AG∥BC．
（2）当OA=$\frac{1}{3}$AB时，⊙O与BC相切，四边形DEOG可以成为菱形．理由如下：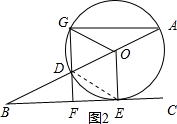
连接DE，如图2所示．
∵∠ABC=30°，∠AGD=90°，
∴GD=$\frac{1}{2}$AD．
要使四边形DEOG成为菱形，则GD与OE平行且相等，
∴OE=$\frac{1}{2}$AD，即OE为⊙O的半径，⊙O与BC相切与点E．
又∵∠ABC=30°，
∴OE=OA=$\frac{1}{2}$OB，即OA=$\frac{1}{3}$AB．

点评 本题考查了菱形的判定、直线与圆的位置关系以及特殊角的三角函数值，解题的关键是：（1）根据平行线的判定证出AG∥BC；（2）找出四边形DEOG为菱形时点O的位置．本题属于中档题，难度不大，解决该题型题目时，根据题意画出图形，数形结合更形象直观．