题目内容
8．
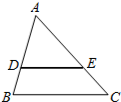如图，在△ABC中，DE∥BC，$\frac{DE}{BC}=\frac{2}{3}$，△ADE的面积是8，则四边形DBCE的面积是10．
分析 根据DE∥BC，于是得到△ADE∽△ABC，根据相似三角形的性质得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{DE}{BC}$）2=$\frac{4}{9}$，由△ADE的面积是8，得到△ABC的面积=18，即可得到结论．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{DE}{BC}$）2=$\frac{4}{9}$，
∵△ADE的面积是8，
∴△ABC的面积=18，
∴四边形DBCE的面积是10．
故答案为：10．
点评 本题考查了相似三角形的性质和判定的应用，熟练地运用性质进行推理是解此题的关键．
练习册系列答案
相关题目
如图，点O是直线AB上一点，OC为任一条射线，OD平分∠AOC，OE平分∠BOC
一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是6．
如图，圆锥体的高h=$\sqrt{3}$cm，底面半径r=1cm，则圆锥体的侧面积为2πcm2．
13．下列实数中是无理数的是（ ）
| A． | 0.38 | B． | $\root{3}{9}$ | C． | $\sqrt{36}$ | D． | -$\frac{22}{7}$ |
20．口袋里有除颜色不同外其它都相同的红、蓝、白三种颜色的小球共30个，摸到红球的概率是$\frac{1}{2}$，摸到蓝球的概率是$\frac{1}{3}$，则袋子里有白球（ ）个．
| A． | 15 | B． | 10 | C． | 5 | D． | 6 |
17．有一组单项式：a2，-$\frac{{a}^{3}}{2}$，$\frac{{a}^{4}}{3}$，-$\frac{{a}^{5}}{4}$…，请观察它们的构成规律，用你发现的规律写出第10个单项式为（ ）
| A． | $\frac{{a}^{10}}{10}$ | B． | -$\frac{{a}^{10}}{10}$ | C． | $\frac{{a}^{11}}{10}$ | D． | -$\frac{{a}^{11}}{10}$ |
18．
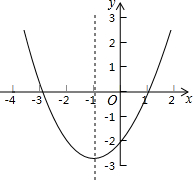已知，二次函数y=ax2+bx+c（a≠0）的图象如图所示，则以下说法不正确的是（ ）
已知，二次函数y=ax2+bx+c（a≠0）的图象如图所示，则以下说法不正确的是（ ）| A． | 根据图象可得该函数y有最小值 | |
| B． | 当x=-2时，函数y的值小于0 | |
| C． | 根据图象可得a＞0，b＜0 | |
| D． | 当x＜-1时，函数值y随着x的增大而减小 |