题目内容
16. 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是6.
一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是6.
分析 根据垂径定理求出BC,根据勾股定理求出OC即可.
解答 解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=$\frac{1}{2}$AB=$\frac{1}{2}$×16=8,
在Rt△OCB中,由勾股定理得:OC=$\sqrt{O{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
故答案为:6.
点评 本题考查了勾股定理和垂径定理的应用;由垂径定理求出BC是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.如果用-10%表示某商品的出口额比上一年减少10%,那么+12%则表示该商品的出口额比上一年( )
| A. | 增加2% | B. | 增加12% | C. | 减少12% | D. | 减少22% |
7.下列计算正确的是( )
| A. | a+a=a2 | B. | 3a2-2a3=1 | C. | 3a3-2a2=a | D. | -a2+2a2=a2 |
4.下列图形中是轴对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
5.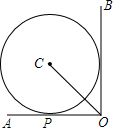 如图,⊙C与∠AOB的两边分别相切,其中OA边与⊙C相切于点P.若∠AOB=90°,OP=6,则OC的长为( )
如图,⊙C与∠AOB的两边分别相切,其中OA边与⊙C相切于点P.若∠AOB=90°,OP=6,则OC的长为( )
 如图,⊙C与∠AOB的两边分别相切,其中OA边与⊙C相切于点P.若∠AOB=90°,OP=6,则OC的长为( )
如图,⊙C与∠AOB的两边分别相切,其中OA边与⊙C相切于点P.若∠AOB=90°,OP=6,则OC的长为( )| A. | 12 | B. | $12\sqrt{2}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
 如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).
如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).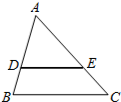 如图,在△ABC中,DE∥BC,$\frac{DE}{BC}=\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是10.
如图,在△ABC中,DE∥BC,$\frac{DE}{BC}=\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是10.