题目内容
3．
如图，圆锥体的高h=$\sqrt{3}$cm，底面半径r=1cm，则圆锥体的侧面积为2πcm2．
分析 根据圆锥的底面半径和高求出圆锥的母线长，再根据圆锥的底面周长等于圆锥的侧面展开扇形的弧长，最后利用扇形的面积计算方法求得侧面积．
解答 解：圆锥的母线长是$\sqrt{（\sqrt{3}）^{2}+{1}^{2}}$=2（cm），
底面周长是2π，
则圆锥体的侧面积是：$\frac{1}{2}$×2×2π=2π（cm2）．
故答案是：2π．
点评 本题考查了圆锥的侧面积的计算方法，解决本题的关键是根据已知条件求出圆锥的母线长和侧面展开扇形的弧长，然后用弧长与母线长乘积的一半求扇形的面积．
练习册系列答案
相关题目
13．如果把分式$\frac{3x}{x+y}$中的x和y的值都扩大5倍，那么分式的值（ ）
| A． | 扩大5倍 | B． | 缩小5倍 | C． | 不改变； | D． | 扩大25倍 |
如图是由五个相同的小正方体搭成的一个几何体，从上面看到的几何体的形状图是（ ）
如图，矩形OABC与矩形ODEF是位似图形，P是位似中心，点B（4，2），E（-2，1），则点P的坐标为（-4，0）．
18．下列函数中，y随x增大而增大的是（ ）
| A． | y=-$\frac{3}{x}$ | B． | y=-x+5 | C． | y=-$\frac{1}{2}$x | D． | y=-$\frac{1}{2}$x2（x＜0） |
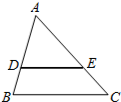如图，在△ABC中，DE∥BC，$\frac{DE}{BC}=\frac{2}{3}$，△ADE的面积是8，则四边形DBCE的面积是10．