题目内容
18.约分(1)$\frac{8ab(x-y)}{{12{a^4}c(y-x)}}$
(2)$\frac{{(a-b){x^{2n}}}}{{(b-a){x^{3n}}}}$
(3)$\frac{{{a^4}-{a^2}{b^2}}}{{{a^2}-ab-2{b^2}}}$
(4)$\frac{{{a^{2n}}{b^{2n}}-{a^{2(n+1)}}}}{{{a^{2n-1}}{b^{2n}}-{a^{2n+1}}}}$.
分析 (1)将分式的分子、分母分别因式分解后约去相同的因式即可;
(2)将分式的分子、分母分别因式分解后约去相同的因式即可;
(3)将分式的分子、分母分别因式分解后约去相同的因式即可;
(4)将分式的分子、分母分别因式分解后约去相同的因式即可.
解答 解:(1)$\frac{8ab(x-y)}{{12{a^4}c(y-x)}}$=$-\frac{2b}{{3{a^3}c}}$;
(2)$\frac{{(a-b){x^{2n}}}}{{(b-a){x^{3n}}}}$=-$\frac{1}{x^n}$;
(3)$\frac{{{a^4}-{a^2}{b^2}}}{{{a^2}-ab-2{b^2}}}$=$\frac{{{a^3}-{a^2}b}}{a-2b}$;
(4)$\frac{{{a^{2n}}{b^{2n}}-{a^{2(n+1)}}}}{{{a^{2n-1}}{b^{2n}}-{a^{2n+1}}}}$=a.
点评 本题考查了约分的知识,解题的关键是对分式的分子与分母分别因式分解,然后约去公因式,分式的约分是分式运算的基础,应重点掌握.

练习册系列答案
相关题目
9.飞机在飞行过程中,如果上升23米记作“+23米”,那么下降15米应记作( )
| A. | -8米 | B. | +8米 | C. | -15米 | D. | +15米 |
6.如果用-10%表示某商品的出口额比上一年减少10%,那么+12%则表示该商品的出口额比上一年( )
| A. | 增加2% | B. | 增加12% | C. | 减少12% | D. | 减少22% |
13.如果把分式$\frac{3x}{x+y}$中的x和y的值都扩大5倍,那么分式的值( )
| A. | 扩大5倍 | B. | 缩小5倍 | C. | 不改变; | D. | 扩大25倍 |
10.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
7.下列计算正确的是( )
| A. | a+a=a2 | B. | 3a2-2a3=1 | C. | 3a3-2a2=a | D. | -a2+2a2=a2 |
 对于三个数a、b、c,M|a,b,c|表示这三个数的平均数,min {a,b,c}表示a、b、c这三个数中最小的数,如:M|-1,2,3|=$\frac{-1+2+3}{3}$=$\frac{4}{3}$,min {-1,2,3}=-1;
对于三个数a、b、c,M|a,b,c|表示这三个数的平均数,min {a,b,c}表示a、b、c这三个数中最小的数,如:M|-1,2,3|=$\frac{-1+2+3}{3}$=$\frac{4}{3}$,min {-1,2,3}=-1;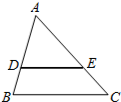 如图,在△ABC中,DE∥BC,$\frac{DE}{BC}=\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是10.
如图,在△ABC中,DE∥BC,$\frac{DE}{BC}=\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是10.