题目内容
19. 如图,点O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC
如图,点O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC(1)写出图中∠AOD和∠AOC的补角;
(2)试说明∠COD和∠COE具有怎样的数量关系,写出证明过程.
分析 (1)根据补角的定义,和是180度的两个角互补,一个角是另一个角的补角;
(2)根据角平分线的定义得到∠DOE=$\frac{1}{2}$∠AOB=90°,据此即可判断.
解答 解:(1)∠AOD的补角是:∠BOD;
∠AOC的补角是∠BOC;
(2)∠COD+∠COE=90°.
理由是:如图,∵OD是∠AOC的角平分线,OE是∠BOC的角平分线,
∴∠COD=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC,
∴∠COD+∠COE=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$×180°=90°.
点评 本题考查了角平分线的定义.根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
相关题目
9.飞机在飞行过程中,如果上升23米记作“+23米”,那么下降15米应记作( )
| A. | -8米 | B. | +8米 | C. | -15米 | D. | +15米 |
10.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
7.下列计算正确的是( )
| A. | a+a=a2 | B. | 3a2-2a3=1 | C. | 3a3-2a2=a | D. | -a2+2a2=a2 |
4.下列图形中是轴对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
 如图是由五个相同的小正方体搭成的一个几何体,从上面看到的几何体的形状图是( )
如图是由五个相同的小正方体搭成的一个几何体,从上面看到的几何体的形状图是( )



 如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).
如图,矩形OABC与矩形ODEF是位似图形,P是位似中心,点B(4,2),E(-2,1),则点P的坐标为(-4,0).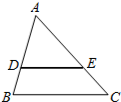 如图,在△ABC中,DE∥BC,$\frac{DE}{BC}=\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是10.
如图,在△ABC中,DE∥BC,$\frac{DE}{BC}=\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是10.


