题目内容
6.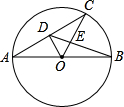 如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.
如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.
分析 连接BC,根据直径所对的圆周角是直角可得∠ACB=90°,然后利用勾股定理列式求出BC,根据垂径定理可得求出CD,再利用勾股定理列式求出BD,然后根据三角形的重心到三角形的顶点的距离等于到中点的距离的2倍求解即可.
解答 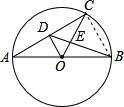 解:如图,连接BC,
解:如图,连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵AC为弦,OD⊥AC于点D,
∴CD=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∵CD、BD是△ABC的中线,
∴点E是△ABC的重心,
∴BE=$\frac{2}{3}$BD=$\frac{2\sqrt{13}}{3}$.
故答案为:$\frac{2\sqrt{13}}{3}$.
点评 本题考查了垂径定理,勾股定理,三角形的重心,综合题难度较大,三角形的重心到三角形的顶点的距离等于到中点的距离的2倍只出现在部分版本教材,此题可以酌情使用.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A. | 3:1:1:3 | B. | 3:3:1:1 | C. | 1:3:3:1 | D. | 1:3:1:3 |
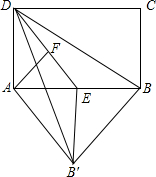 在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.
在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.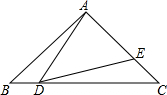 如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;
如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;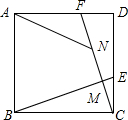 如图,E,F分别是边长为6的正方形ABCD的边CD,AD上两点,且CE=DF,连接CF,BE交于点M,在MF上截取MN=MC,连接AN,若FN=$\frac{4}{3}$CM,则AN的长度为$\frac{12\sqrt{5}}{5}$.
如图,E,F分别是边长为6的正方形ABCD的边CD,AD上两点,且CE=DF,连接CF,BE交于点M,在MF上截取MN=MC,连接AN,若FN=$\frac{4}{3}$CM,则AN的长度为$\frac{12\sqrt{5}}{5}$.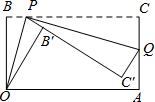 已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为
已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为