题目内容
16.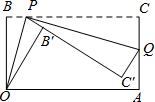 已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为
已知一个矩形纸片OACB,OB=6,OA=11,点P为BC边上的动点(点P不与点B,C重合),经过点O折叠该纸片,得折痕OP和点B′,经过点P再次折叠纸片,使点C落在直线PB′上,得折痕PQ和点C′,当点C′恰好落在边OA上时BP的长为$\frac{11+\sqrt{13}}{3}$或$\frac{11-\sqrt{13}}{3}$.
分析 设BP=t,AQ=m,首先过点P作PE⊥OA于E,易证△PC′E∽△C′QA,由勾股定理可求得C′Q的长,然后利用相似三角形的对应边成比例得到m=$\frac{1}{6}$t2-$\frac{11}{6}$t+6,即可求得t的值.
解答  解:过点P作PE⊥OA于E,
解:过点P作PE⊥OA于E,
∴∠PEA=∠QAC′=90°,
∴∠PC′E+∠EPC′=90°,
∵∠PC′E+∠QC′A=90°,
∴∠EPC′=∠QC′A,
∴△PC′E∽△C′QA,
∴$\frac{PE}{AC′}$=$\frac{PC′}{C′Q}$,
设BP=t,AQ=m,
∵PC′=PC=11-t,PE=OB=6,C′Q=CQ=6-m,
AC′=$\sqrt{C{′Q}^{2}-{AQ}^{2}}$=$\sqrt{36-12m}$,
∴$\frac{6}{\sqrt{36-12m}}$=$\frac{11-t}{6-m}$.
∵$\frac{11-t}{6-m}$=$\frac{6}{t}$,
∴m=$\frac{1}{6}$t2-$\frac{11}{6}$t+6,
又∵36-12m=t2,
将m=$\frac{1}{6}$t2-$\frac{11}{6}$t+6代入36-12m=t2,
化简得,3t2-22t+36=0,
解得:t1=$\frac{11+\sqrt{13}}{3}$,t2=$\frac{11-\sqrt{13}}{3}$.
故答案为:$\frac{11+\sqrt{13}}{3}$或$\frac{11-\sqrt{13}}{3}$.
点评 本题主要考查了图形的折叠问题,矩形的性质、相似三角形的判定与性质以及运用数形结合思想列方程的综合运用,运用相似的性质列比例式得出方程求出BP是解决问题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
7.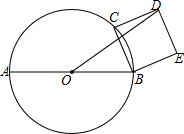 如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
 如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )| A. | 随点C的运动而变化,最大值为2+2$\sqrt{2}$ | B. | 不变 | ||
| C. | 随点C的运动而变化,最大值为2$\sqrt{2}$ | D. | 随点C的运动而变化,但无最值 |
4.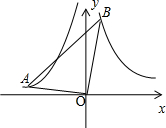 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3}{2}$ |
11.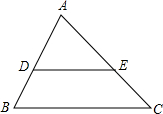 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
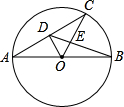 如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.
如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.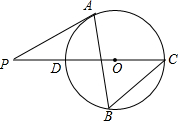 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.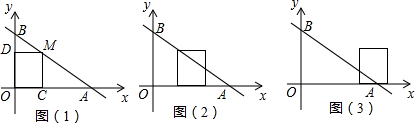
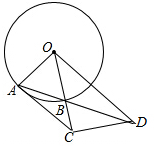 已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.
已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.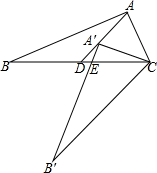 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.
如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.