题目内容
1.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )| A. | 3:1:1:3 | B. | 3:3:1:1 | C. | 1:3:3:1 | D. | 1:3:1:3 |
分析 根据平行四边形的对角相等即可判断.
解答 解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D.
故选D.
点评 本题考查平行四边形的性质,利用平行四边形的对角相等解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | b3•b4=b7 | B. | (b3)4=b7 | C. | b3+b4=b7 | D. | b6÷b3=b2 |
12.如果一个多边形的每一个内角都相等,且每一个内角的度数为135°,那么这个多边形的边数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 以上答案都不对 |
16.下列各式中,是分式的是( )
| A. | $\frac{{x}^{2}+1}{2}$ | B. | $\frac{3xy}{π}$ | C. | $\frac{3}{xy}$ | D. | $\frac{m-n}{5}$ |
4.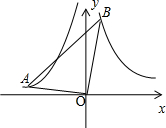 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3}{2}$ |
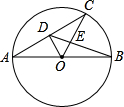 如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.
如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.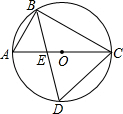 如图.AC是⊙O的直径,点B在⊙O上,∠ACB=30°.作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比.
如图.AC是⊙O的直径,点B在⊙O上,∠ACB=30°.作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比.