题目内容
7．$\sqrt{{x}^{2}+{y}^{2}-2xy-14x+14y+49}$+$\frac{1}{5}$$\sqrt{2x-3y+5}$=0，试求x2-y2的值．分析 根据几个非负数的和的性质得到x2+y2-2xy-14x+14y+49=0，2x-3y+5=0，再利用配方法由x2+y2-2xy-14x+14y+49=0得（x-y-7）2=0，则x-y-7=0，然后解方程组$\left\{\begin{array}{l}{2x-3y+5=0}\\{x-y-7=0}\end{array}\right.$得x和y的值，再利用平方差公式计算x2-y2的值．
解答 解：根据题意得x2+y2-2xy-14x+14y+49=0，2x-3y+5=0，
由x2+y2-2xy-14x+14y+49=0得（x+y）2-14（x-y）+49=0，所以（x-y-7）2=0，则x-y-7=0，
解方程组$\left\{\begin{array}{l}{2x-3y+5=0}\\{x-y-7=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=26}\\{y=19}\end{array}\right.$，
所以x2-y2=262-192=315．
点评 本题考查了非负数的性质：算术平方根具有非负性．非负数之和等于0时，各项都等于0，利用此性质列方程解决求值问题．
练习册系列答案
阅读快车系列答案
相关题目
13．用配方法解方程3x2-$\frac{12}{5}$x-1=0时，变形正确的是（ ）
| A． | （x+$\frac{2}{5}$）2-$\frac{37}{25}$=0 | B． | 3（x+$\frac{2}{5}$）2-$\frac{37}{25}$=0 | C． | （x-$\frac{2}{5}$）2-$\frac{37}{25}$=0 | D． | 3（x-$\frac{2}{5}$）2-$\frac{37}{25}$=0 |
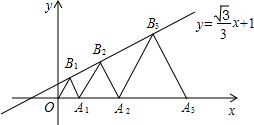如图，点A1、A2、A3、…在平面直角坐标系x轴上，点B1、B2、B3、…在直线y=$\frac{\sqrt{3}}{3}$x+1上，△OA1B1、△A1B2A2、△A2B3A3…均为等边三角形．则A2016的横坐标为22016$\sqrt{3}$-$\sqrt{3}$．
12．在△ABC中，若|sinB-$\frac{\sqrt{2}}{2}$|+$\sqrt{1-tanA}$=0，则△ABC是（ ）
| A． | 锐角三角形 | B． | 钝角三角形 | C． | 直角三角形 | D． | 等腰直角三角形 |
