题目内容
19．已知$\sqrt{x-\frac{1}{2}}$+|y-3|+（z+8）2=0，求zxy的值．分析 直接利用绝对值以及偶次方的性质和二次根式的性质得出x，y，z的值，进而得出答案．
解答 解：∵$\sqrt{x-\frac{1}{2}}$+|y-3|+（z+8）2=0，
∴x=$\frac{1}{2}$，y=3，z=-8，
∴zxy=（-8）×（$\frac{1}{2}$）3=-1．
点评 此题主要考查了偶次方的性质以及绝对值的性质和二次根式的性质，正确得出x，y，z的值是解题关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
5．下列选项中正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ | C． | $\frac{n}{m}$=$\frac{n-a}{m-a}$ | D． | 若a＞0，则$\sqrt{a^2}=a$ |
4．若直线y1=m2x+a与直线y2=-2x+b的交点坐标为（1，2），则使y1＜y2成立的x的取值范围为（ ）
| A． | x＞1 | B． | x＞2 | C． | x＜1 | D． | x＜2 |
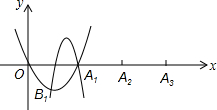如图，已知在平面直角坐标系中，x轴上依次有点A1（2，0），A2（4，0），A3（6，0），…，抛物线l1：y=x2+bx+c经过原点及A1，顶点为B1；抛物线l2经过B1和A1，且形状与抛物线l1的形状相同，开口方向相反；抛物线l3经过A1和A2，且形状与抛物线l2的形状相同，开口方向相反，顶点为B2：抛物线l4经过B2和A2，且形状与抛物线l3的形状相同，开口方向相反：抛物线l5经过A2和A3，且形状与抛物线l4的形状相同，开口方向相反，顶点为B3：依此类推…