题目内容
16. 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.(1)求证:四边形DEFG是平行四边形;
(2)当OA=BC时,求证:四边形DEFG是菱形.
分析 (1)首先利用三角形中位线的性质得出DE∥BC,DE=$\frac{1}{2}$BC,同理,GF∥BC,GF=$\frac{1}{2}$BC,即可得出DE∥GF,DE=GF即可得出四边形DGFE是平行四边形;
(2)利用(1)中所求,只要邻边再相等即可得出答案.
解答 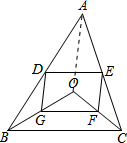 (1)证明:∵D、E分别是边AB、AC的中点.
(1)证明:∵D、E分别是边AB、AC的中点.
∴DE∥BC,DE=$\frac{1}{2}$BC.
同理,GF∥BC,GF=$\frac{1}{2}$BC.
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形.
(2)证明:如图,连接OA.由(1)得出四边形DEFG是平行四边形,
∵AO=BC,
∴GD=$\frac{1}{2}$AO,GF=$\frac{1}{2}$BC,
∴DG=GE,
∴平行四边形DEFG是菱形.
点评 此题主要考查了中点四边形的判定以及三角形的中位线的性质和平行四边形以及菱形的判定等知识,熟练掌握相关的定理是解题关键.

练习册系列答案
相关题目
6. 如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )
如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )
 如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )
如图,在Rt△ABC中,CD是边AB上的高,若AC=4,AB=10,则AD的长为( )| A. | $\frac{8}{5}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
1.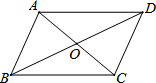 如图,下列四组条件中,能判定?ABCD是正方形的有( )
如图,下列四组条件中,能判定?ABCD是正方形的有( )
①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.
 如图,下列四组条件中,能判定?ABCD是正方形的有( )
如图,下列四组条件中,能判定?ABCD是正方形的有( )①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.若正比例函数y=kx(k≠0)的图象经过(-1,3),则k的值为( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
4.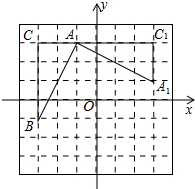 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )
 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )| A. | (0,0) | B. | (-1,0) | C. | (1,0) | D. | (0,-1) |
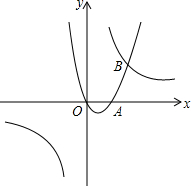 经过原点和点A(2,0)的抛物线y=ax2+bx+c与双曲线y=$\frac{k}{x}$交于B(3,3).
经过原点和点A(2,0)的抛物线y=ax2+bx+c与双曲线y=$\frac{k}{x}$交于B(3,3).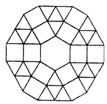 如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.
如图是某广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖铺设,从里向外共铺了12层(不包括中央的正六边形地砖),每一层的外边界都围成一个多边形,若中央正六边形的地砖的边长为0.5m,则第12层的外边界所围成的多边形的周长是39m.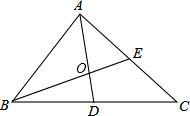 如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA=10.
如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA=10.