题目内容
5.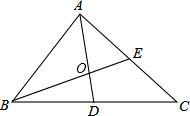 如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA=10.
如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA=10.
分析 根据三角形的重心到顶点的长度等于到对边中点的长度的2倍可得OD=$\frac{1}{2}$AO,再根据等高的三角形的面积等于底边的比求出△AOB的面积.
解答 解:∵中线AD、BE相交于点O,
∴O是△ABC的重心,
∴OD=$\frac{1}{2}$AO,
∵S△BOD=5,
∴S△AOB=2S△BOD=2×5=10.
故答案为:10.
点评 本题考查了三角形的重心,三角形的重心到顶点的长度等于到对边中点的长度的2倍,等高的三角形的面积等于底边的比是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.如图1,一根长30cm、宽3cm的长方形纸条,将它按照图2所示的过程折叠,为了美观,希望折叠完成后纸条A端到点P的距离等于B端到点M的距离,则最初折叠时,MA的长应为( )
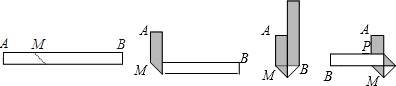

| A. | 7.5cm | B. | 9cm | C. | 10.5cm | D. | 12cm |
10.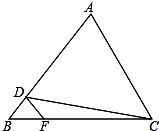 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:24 |
14.某校对该校八(1)班学生上学期期末考试数学成绩(成绩取整数,满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分别直方图和频数、频率分别表,请你根据图表提供的信息,解答下列问题:
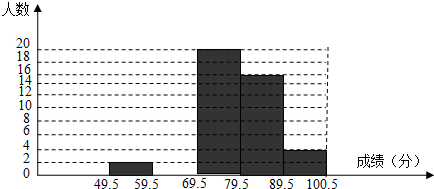
(1)频数、频率分布表中a=8,b=0.08;(答案直接填在题中横线上 )
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | A | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | B | 1 |

(1)频数、频率分布表中a=8,b=0.08;(答案直接填在题中横线上 )
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
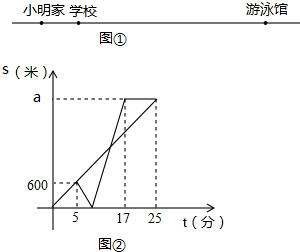 图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.
图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.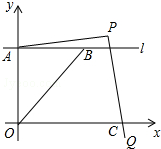 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.