题目内容
7.小玉同学在进行多边形内角和的计算时,求得一个多边形的内角和为1350°,当她发现算错之后进行检查,原来多加了一个外角,你知道她多加的这个外角是多少度吗?分析 根据多边形的内角和公式(n-2)•180°可知,多边形的内角和是180°的倍数,再根据多边形的每一个外角大于0°且小于180°即可求出多加的外角的度数.
解答 解:设多边形的边数为n,多加的外角度数为α,则
(n-2)•180°=1350°-α,
∵1350°=7×180°+90°,内角和应是180°的倍数,
∴小玉同学多加的一个外角为90°.
点评 本题考查了多边形的内角和公式,根据多边形的内角和公式判断出多边形的内角和是180°的倍数是解题的关键.

练习册系列答案
相关题目
12. 如图,∠AOB=∠BOC,且∠BOC:∠COD:∠DOA=2:5:3,则∠AOB=( )
如图,∠AOB=∠BOC,且∠BOC:∠COD:∠DOA=2:5:3,则∠AOB=( )
 如图,∠AOB=∠BOC,且∠BOC:∠COD:∠DOA=2:5:3,则∠AOB=( )
如图,∠AOB=∠BOC,且∠BOC:∠COD:∠DOA=2:5:3,则∠AOB=( )| A. | 30° | B. | 36° | C. | 40° | D. | 60° |
16.如图1,一根长30cm、宽3cm的长方形纸条,将它按照图2所示的过程折叠,为了美观,希望折叠完成后纸条A端到点P的距离等于B端到点M的距离,则最初折叠时,MA的长应为( )
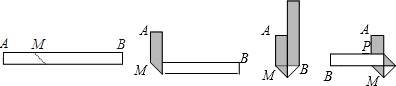

| A. | 7.5cm | B. | 9cm | C. | 10.5cm | D. | 12cm |
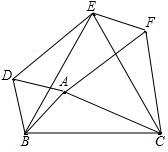 如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF.
如图,已知以△ABC的三边为边,在BC的同侧分别作等边三角形ABD、BCE和ACF. 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.