题目内容
8.若正比例函数y=kx(k≠0)的图象经过(-1,3),则k的值为( )| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
分析 因为正比例函数y=kx(k≠0)的图象经过(-1,3),代入解析式,解之即可求得k.
解答 解:∵正比例函数y=kx(k≠0)的图象经过(-1,3),
∴3=-k,
解得:k=-3.
故选B.
点评 此题考查了待定系数法求一次函数的解析式,需灵活运用待定系数法建立函数解析式,然后将点的坐标代入解析式,利用方程解决问题.

练习册系列答案
相关题目
13.下列运算中正确的是( )
| A. | $\root{3}{-3}=-\root{3}{-3}$ | B. | $\root{3}{-3}=\root{3}{3}$ | C. | $\root{3}{-3}=\root{3}{{|{-3}|}}$ | D. | $\root{3}{-3}=-\root{3}{3}$ |
16.如图1,一根长30cm、宽3cm的长方形纸条,将它按照图2所示的过程折叠,为了美观,希望折叠完成后纸条A端到点P的距离等于B端到点M的距离,则最初折叠时,MA的长应为( )
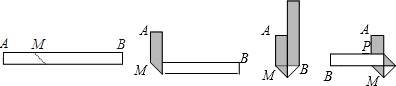

| A. | 7.5cm | B. | 9cm | C. | 10.5cm | D. | 12cm |
 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.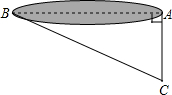 如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上点,测得BC=60m,AC=20m,则A,B两点问的距离40$\sqrt{2}$m.
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上点,测得BC=60m,AC=20m,则A,B两点问的距离40$\sqrt{2}$m.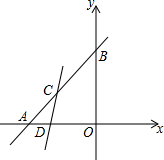 如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1
如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1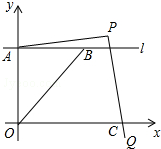 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.