题目内容
已知多边形的一个内角的外角与其余各内角的度数之和为450°,求这个多边形的边数.
考点:多边形内角与外角
专题:
分析:根据n边形的内角和定理可知:n边形内角和为(n-2)×180°.设这个外角度数为x度,利用方程即可求出答案.
解答:解:设这个外角度数为x,根据题意,得
(n-2)×180°+x=450°,
解得:x=450°-180°n+360°=810°-180°n,
由于0<x<180°,即0<810°-180°n<180°,
解得
<n<
,
所以n=4.
故多边形的边数是4.
(n-2)×180°+x=450°,
解得:x=450°-180°n+360°=810°-180°n,
由于0<x<180°,即0<810°-180°n<180°,
解得
| 7 |
| 2 |
| 9 |
| 2 |
所以n=4.
故多边形的边数是4.
点评:主要考查了多边形的内角和定理.n边形的内角和为:180°•(n-2).

练习册系列答案
相关题目
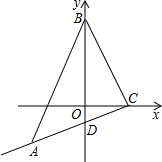 如图,在平面直角坐标系中,点C(3,0)在x轴的正半轴上,点B(0,3
如图,在平面直角坐标系中,点C(3,0)在x轴的正半轴上,点B(0,3 如图所示,在△ABC中,BD、CE分别是AC、AB上的高,连接DE,试说明△ADE∽△ABC.
如图所示,在△ABC中,BD、CE分别是AC、AB上的高,连接DE,试说明△ADE∽△ABC. 某商场举行店庆酬宾促销活动,商场规定:顾客每购买99元的商品,就能获得一次抽奖的机会,如果顾客不愿意抽奖,可以直接获得购物券10元.商场内设立了多个抽奖点,为了吸引顾客商场电子屏实时显示抽奖状况,下面是一位顾客用手机拍下的电子屏画面:
某商场举行店庆酬宾促销活动,商场规定:顾客每购买99元的商品,就能获得一次抽奖的机会,如果顾客不愿意抽奖,可以直接获得购物券10元.商场内设立了多个抽奖点,为了吸引顾客商场电子屏实时显示抽奖状况,下面是一位顾客用手机拍下的电子屏画面: