题目内容
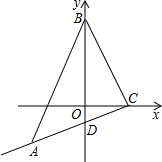 如图,在平面直角坐标系中,点C(3,0)在x轴的正半轴上,点B(0,3
如图,在平面直角坐标系中,点C(3,0)在x轴的正半轴上,点B(0,3| 2 |
(1)求点A的坐标;
(2)在y轴上有一动点E以每秒
| 2 |
(3)请问:此时射线BD是否平分∠ABC?若是,请证明;若不是,请说明理由.
考点:一次函数综合题
专题:
分析:(1)作AM⊥x轴于M,根据AAS即可证得△AMC≌△COB得出AM=OC,CM=OB,进而得出A的坐标;
(2)根据A、C的坐标求得直线AC的解析式,从而求得D的坐标,得出ED的长,然后根据三角形的面积公式,即可得出S与t的关系式;
(3)根据A、B的坐标,求得直线AB的解析式,从而求得直线AB与x轴的交点E的坐标,得出OE=OC,根据垂直平分线上的点,到线段的两个端点的距离相等,求得三角形BEC是等腰三角形,进而求得BD是∠ABC的平分线.
(2)根据A、C的坐标求得直线AC的解析式,从而求得D的坐标,得出ED的长,然后根据三角形的面积公式,即可得出S与t的关系式;
(3)根据A、B的坐标,求得直线AB的解析式,从而求得直线AB与x轴的交点E的坐标,得出OE=OC,根据垂直平分线上的点,到线段的两个端点的距离相等,求得三角形BEC是等腰三角形,进而求得BD是∠ABC的平分线.
解答: (1)解:作AM⊥x轴于M,
(1)解:作AM⊥x轴于M,
∵点C(3,0),B(0,3
+3),
∴OC=3,OB=3
+3,
∵∠BCO+∠OCD=90°,∠OBC+∠BCO=90°,
∴∠MCA=∠OBC,
在△AMC与△COB中,
,
∴△AMC≌△COB(AAS)
∴AM=OC=23,CM=OB=3
+3,
∴A(-3
,-3),
(2)解:∵A(-3
,-3),C(3,0),B(0,3
+3),
∴直线AC为:y=(
-1)x+3-3
,
∴D(0,3-3
),
∴BD=3
+3-(3-3
)=6
,
∵BE=2t,
∴DE=6
-2t,
∴S=
DE•3
=
(6
-2t)×3
=18-3
t,
即S=18-3
t;
(3)证明:∵A(-3
,-3),C(3,0),B(0,3
+3),
∴直线AB为:y=(
+1)x+3
+3,
令y=0,x=-3,
∴E(-3,0),
∵C(3,0),
∴OE=OC,
∵OB⊥CE,
∴BE=CB,
∴△BEC是等腰三角形,
∴BD平分∠ABC.
 (1)解:作AM⊥x轴于M,
(1)解:作AM⊥x轴于M,∵点C(3,0),B(0,3
| 2 |
∴OC=3,OB=3
| 2 |
∵∠BCO+∠OCD=90°,∠OBC+∠BCO=90°,
∴∠MCA=∠OBC,
在△AMC与△COB中,
|
∴△AMC≌△COB(AAS)
∴AM=OC=23,CM=OB=3
| 2 |
∴A(-3
| 2 |
(2)解:∵A(-3
| 2 |
| 2 |
∴直线AC为:y=(
| 2 |
| 2 |
∴D(0,3-3
| 2 |
∴BD=3
| 2 |
| 2 |
| 2 |
∵BE=2t,
∴DE=6
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
即S=18-3
| 2 |
(3)证明:∵A(-3
| 2 |
| 2 |
∴直线AB为:y=(
| 2 |
| 2 |
令y=0,x=-3,
∴E(-3,0),
∵C(3,0),
∴OE=OC,
∵OB⊥CE,
∴BE=CB,
∴△BEC是等腰三角形,
∴BD平分∠ABC.
点评:本题考查了三角形全等的判定和性质,直线和x轴的交点,以及等腰三角形的判定和性质,本题的关键是直线与坐标轴的交点坐标.

练习册系列答案
相关题目
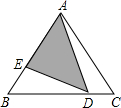 如图,△ABC的面积为1cm2,BD=2CD,AE=2BE,求阴影部分的面积.
如图,△ABC的面积为1cm2,BD=2CD,AE=2BE,求阴影部分的面积.