题目内容
若△ABC三边长a,b,c,满足|a-41|+|b-9|+|c-40|=0,试说明△ABC是直角三角形.
考点:勾股定理的逆定理,非负数的性质:绝对值
专题:
分析:先根据非负数的性质求出a、b、c的值,再根据勾股定理的逆定理判断出△ABC的形状即可.
解答:解:∵|a-41|+|b-9|+|c-40|=0,
∴a-41=0,b-9=0,c-40=0,
∴a=41,b=9,c=40.
∵92+402=1681=412,即b2+c2=a2,
∴△ABC是直角三角形.
∴a-41=0,b-9=0,c-40=0,
∴a=41,b=9,c=40.
∵92+402=1681=412,即b2+c2=a2,
∴△ABC是直角三角形.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图所示:O为坐标原点,点A坐标是(3,1).线段OA绕原点O逆时针旋转90°后得到点B.
如图所示:O为坐标原点,点A坐标是(3,1).线段OA绕原点O逆时针旋转90°后得到点B. 已知梯形ABCD里,AB∥DC,AD=BC,AC、BD交于O,若BD=10,∠DOC=120°,求梯形ABCD的面积.
已知梯形ABCD里,AB∥DC,AD=BC,AC、BD交于O,若BD=10,∠DOC=120°,求梯形ABCD的面积. 如图,点O是△ABC内的一点,证明:OA+OB+OC>
如图,点O是△ABC内的一点,证明:OA+OB+OC>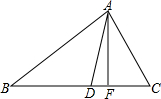 AF、AD分别是△ABC的高和角平分线,且∠B=30°,∠C=56°,求∠DAF的度数.
AF、AD分别是△ABC的高和角平分线,且∠B=30°,∠C=56°,求∠DAF的度数.