题目内容
1.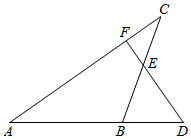 如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )| A. | ∠FEC=45° | B. | BE=DE | C. | AB=BC | D. | AB=DF |
分析 由题中已知条件,DF⊥AC,BD=BE,因此,可以通过角的加减求得∠A与∠C相等,从而得出AB=BC.
解答 解:∵DF⊥AC,
∴∠DFA=∠EFC=90°.
∴∠A=∠DFA-∠D,∠C=∠EFC-∠CEF,
∵BD=BE,
∴∠BED=∠D.
∵∠BED=∠CEF,
∴∠D=∠CEF.
∴∠A=∠C.
∴AB=BC;
故选:C.
点评 本题考查了等腰三角形的判定、直角三角形的性质以及对顶角相等的性质;证出∠A=∠C是解决问题的关键.

练习册系列答案
相关题目
12.化简:$(\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}})^{2}$的结果是( )
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 4 | D. | -4$\sqrt{2}$ |
16.一个自然数a的算术平方根为x,那么a+2的算术平方根为( )
| A. | x+2 | B. | x2+2 | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{x}$+2 |
13.下列各式是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{3x}$ | C. | $\sqrt{{2x}^{3}}$ | D. | $\sqrt{\frac{5}{3}}$ |
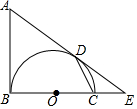 如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E.
如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD、BC的延长线相交于点E.