题目内容
12.化简:$(\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}})^{2}$的结果是( )| A. | 6 | B. | 4$\sqrt{2}$ | C. | 4 | D. | -4$\sqrt{2}$ |
分析 根据二次根式的性质即可求出答案.
解答 解:原式=3+2$\sqrt{2}$-2$\sqrt{(3+2\sqrt{2})(3-2\sqrt{2})}$+3-2$\sqrt{2}$
=6-2$\sqrt{9-8}$
=6-2
=4
故选(C)
点评 本题考查二次根式的性质,解题的关键是熟练运用二次根式的运算法则,本题属于基础题型.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
17.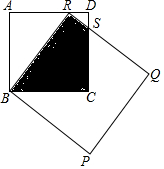 如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )
如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )
 如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )
如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )| A. | 8 | B. | $\frac{17}{2}$ | C. | $\frac{28}{3}$ | D. | $\frac{77}{8}$ |
1.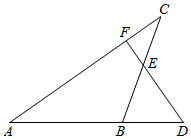 如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
 如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )| A. | ∠FEC=45° | B. | BE=DE | C. | AB=BC | D. | AB=DF |
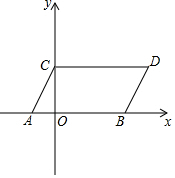 如图,在平面直角坐标系中,A(-1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.
如图,在平面直角坐标系中,A(-1,0),B(3,0),C(0,2),CD∥x轴,CD=AB. 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=32cm,△OAB的周长是22cm,则EF=3cm.
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=32cm,△OAB的周长是22cm,则EF=3cm.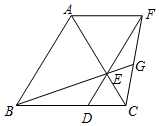 如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.
如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.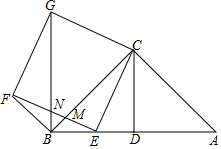 已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.
已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.