题目内容
17.解分式方程:(1)$\frac{2x}{x+2}$-$\frac{3}{x-2}$=2
(2)$\frac{2}{1+x}$-$\frac{3}{1-x}$=$\frac{6}{{x}^{2}-1}$.
分析 (1)先把分式方程化为整式方程2x(x-2)-3(x+2)=2(x+2)(x-2),再解整式方程,然后进行检验确定原方程的解;
(2)先把分式方程化为整式方程得2(x-1)+3(x+1)=6,再解整式方程,然后进行检验确定原方程的解.
解答 解:(1)去分母得2x(x-2)-3(x+2)=2(x+2)(x-2),
解得x=$\frac{2}{7}$,
经检验,x=$\frac{2}{7}$为原方程的根;
(2)$\frac{2}{x+1}$+$\frac{3}{x-1}$=$\frac{6}{(x+1)(x-1)}$
去分母得2(x-1)+3(x+1)=6,
解得x=1,
经检验,x=1为原方程的增根,
所以原方程无解.
点评 本题考查了解分式方程:熟练掌握解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.

练习册系列答案
相关题目
1.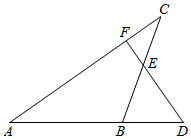 如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
 如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )| A. | ∠FEC=45° | B. | BE=DE | C. | AB=BC | D. | AB=DF |
5.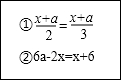 数学老师在如图所示的木板上写了关于x的两个方程,并解出方程①的解比方程②的解小4,则a的值为( )
数学老师在如图所示的木板上写了关于x的两个方程,并解出方程①的解比方程②的解小4,则a的值为( )
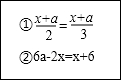 数学老师在如图所示的木板上写了关于x的两个方程,并解出方程①的解比方程②的解小4,则a的值为( )
数学老师在如图所示的木板上写了关于x的两个方程,并解出方程①的解比方程②的解小4,则a的值为( )| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | 2 | D. | -2 |
7.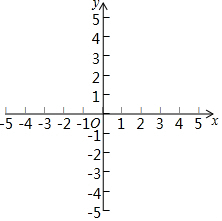 数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$图象与性质.小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:
数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$图象与性质.小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:
(1)函数y=$\frac{x}{x+1}$的自变量x的取值范围是x≠-1;
(2)根据下表所列出y与x对应值,在平面直角坐标系中描出各对以对应值为坐标的点,并画出该函数的图象;
(3)若直线y=x+b与函数y=$\frac{x}{x+1}$的图象无交点,请直接写出b的取值范围.
 数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$图象与性质.小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:
数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$图象与性质.小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:(1)函数y=$\frac{x}{x+1}$的自变量x的取值范围是x≠-1;
(2)根据下表所列出y与x对应值,在平面直角坐标系中描出各对以对应值为坐标的点,并画出该函数的图象;
(3)若直线y=x+b与函数y=$\frac{x}{x+1}$的图象无交点,请直接写出b的取值范围.
| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=32cm,△OAB的周长是22cm,则EF=3cm.
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=32cm,△OAB的周长是22cm,则EF=3cm.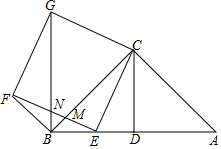 已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.
已知△ABC为等腰直角三角形,∠ACB=90°,CD是斜边AB上的中线,且CD=2,点E是线段BD上任意一点,以CE为边向左侧作正方形CEFG,EF交BC于点M,连接BG交EF于点N.