题目内容
8.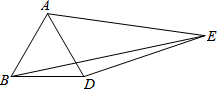 如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )
如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )| A. | 4 | B. | $\sqrt{13}$ | C. | 5 | D. | $\sqrt{15}$ |
分析 如图,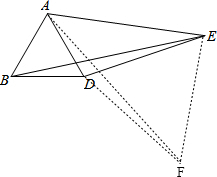 ,作EF⊥AE,且EF=DE,连接AF、DF;然后根据三角形全等的判定方法,判断出△ADF≌△BDE,所以BE=AF;最后在直角三角形AEF中,根据勾股定理,求出AF的长度,即可求出BE的长为多少.
,作EF⊥AE,且EF=DE,连接AF、DF;然后根据三角形全等的判定方法,判断出△ADF≌△BDE,所以BE=AF;最后在直角三角形AEF中,根据勾股定理,求出AF的长度,即可求出BE的长为多少.
解答 解:如图, ,
,
作EF⊥AE,且EF=DE,连接AF、DF,
因为∠AEF=90°,
所以∠DEF=90-30=60°,DE=EF,
所以△DEF是等边三角形,
所以∠EDF=60°,∠ADF=∠BDE,
因为AD=BD,DE=EF,∠ADF=∠BDE,
所以△BDE≌△ADF,
所以BE=AF=$\sqrt{{3}^{2}{+2}^{2}}=\sqrt{13}$.
故选:B.
点评 此题主要考查了全等三角形的判断方法和性质,以及等边三角形的特征、勾股定理的应用,要熟练掌握,解答此题的关键是判断出:△BDE≌△ADF,进而判断出BE的长等于AF的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.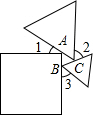 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 130° | D. | 180° |
20.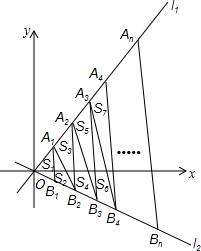 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )| A. | $\frac{2016\sqrt{3}}{3}$ | B. | 1008$\sqrt{3}$ | C. | $\frac{2015\sqrt{3}}{2}$ | D. | $\frac{2015\sqrt{3}}{3}$ |
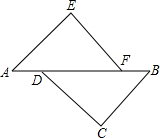 如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.
如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.