题目内容
3.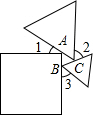 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 130° | D. | 180° |
分析 设围成的小三角形为△ABC,分别用∠1、∠2、∠3表示出△ABC的三个内角,再利用三角形的内角和等于180°列式整理即可得解.
解答  解:如图,∠BAC=180°-90°-∠1=90°-∠1,
解:如图,∠BAC=180°-90°-∠1=90°-∠1,
∠ABC=180°-60°-∠3=120°-∠3,
∠ACB=180°-60°-∠2=120°-∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°-∠1+120°-∠3+120°-∠2=180°,
∴∠1+∠2=150°-∠3,
∵∠3=50°,
∴∠1+∠2=150°-50°=100°.
故选:A.
点评 本题考查了三角形的内角和定理,用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键,也是本题的难点.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
13. 如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
 如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )| A. | 46° | B. | 92° | C. | 44° | D. | 23° |
8.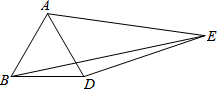 如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )
如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )
 如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )
如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )| A. | 4 | B. | $\sqrt{13}$ | C. | 5 | D. | $\sqrt{15}$ |
 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标.
如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标.