题目内容
20.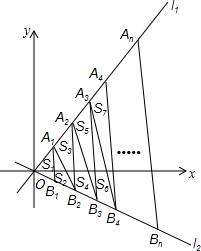 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )| A. | $\frac{2016\sqrt{3}}{3}$ | B. | 1008$\sqrt{3}$ | C. | $\frac{2015\sqrt{3}}{2}$ | D. | $\frac{2015\sqrt{3}}{3}$ |
分析 根据一次函数图象上点的坐标特征得到A1(1,$\sqrt{3}$),B1(1,-$\frac{\sqrt{3}}{3}$),于是可判断直线y1=$\sqrt{3}$x与x轴的夹角为60°,直线y2=-$\frac{\sqrt{3}}{3}$x与x轴的夹角为30°,则l1⊥l2,根据特殊角的三角函数值可得到OA1=2,OA2=4,OA3=6,OA4=8,OB1=$\frac{2\sqrt{3}}{3}$,OB2=$\frac{4\sqrt{3}}{3}$,OB3=2$\sqrt{3}$,OB4=$\frac{8\sqrt{3}}{3}$,所以OA1=A1A2=A2A3=A3A4=2,OB1=B1B2=B2B3=B3B4=$\frac{2\sqrt{3}}{3}$,接着根据三角形面积公式可计算出S1=$\frac{2\sqrt{3}}{3}$,S2=$\frac{2\sqrt{3}}{3}$,S3=$\frac{4\sqrt{3}}{3}$,S4=$\frac{4\sqrt{3}}{3}$,S5=$\frac{6\sqrt{3}}{3}$,S6=$\frac{6\sqrt{3}}{3}$,按此规律可得S2015=$\frac{2016\sqrt{3}}{3}$,S2016=$\frac{2016\sqrt{3}}{3}$.
解答 解:当x=1时,y1=$\sqrt{3}$x=$\sqrt{3}$,y2=-$\frac{\sqrt{3}}{3}$x=-$\frac{\sqrt{3}}{3}$,则A1(1,$\sqrt{3}$),B1(1,-$\frac{\sqrt{3}}{3}$),
则直线y1=$\sqrt{3}$x与x轴的夹角为60°,直线y2=-$\frac{\sqrt{3}}{3}$x与x轴的夹角为30°,
所以l1⊥l2,
同样可得A2(2,2$\sqrt{3}$),B2(2,-$\frac{2\sqrt{3}}{3}$),A3(3,3$\sqrt{3}$),B3(3,-$\sqrt{3}$),A4(4,4$\sqrt{3}$),B1(4,-$\frac{4\sqrt{3}}{3}$),
所以OA1=2,OA2=4,OA3=6,OA4=8,OB1=$\frac{2\sqrt{3}}{3}$,OB2=$\frac{4\sqrt{3}}{3}$,OB3=2$\sqrt{3}$,OB4=$\frac{8\sqrt{3}}{3}$,
则OA1=A1A2=A2A3=A3A4=2,OB1=B1B2=B2B3=B3B4=$\frac{2\sqrt{3}}{3}$,
所以S1=$\frac{1}{2}$OA1•OB1=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
S2=$\frac{1}{2}$OA1•B1B2=$\frac{1}{2}$×2×$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
S3=$\frac{1}{2}$A1A2•OB2=$\frac{1}{2}$×2×$\frac{4\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
S4=$\frac{1}{2}$OA2•B2B3=$\frac{1}{2}$×4×$\frac{2\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
S5=$\frac{1}{2}$A2A3•OB3=$\frac{1}{2}$×2×2$\sqrt{3}$=$\frac{6\sqrt{3}}{3}$,
S6=$\frac{1}{2}$OA3•B3B4=$\frac{1}{2}$×6×$\frac{2\sqrt{3}}{3}$=$\frac{6\sqrt{3}}{3}$,
…
所以S2015=$\frac{2016\sqrt{3}}{3}$,
S2016=$\frac{2016\sqrt{3}}{3}$.
故选A.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b(k≠0,且k,b为常数)的图象是一条直线.直线上任意一点的坐标都满足函数关系式y=kx+b.找到直线y1=$\sqrt{3}$x与y2=-$\frac{\sqrt{3}}{3}$x和x轴的夹角是解决此题的关键.

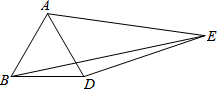 如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )
如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )| A. | 4 | B. | $\sqrt{13}$ | C. | 5 | D. | $\sqrt{15}$ |
 正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )
正方形ABCD的位置在坐标系中如图,点A、D的坐标分别为(1,0)、(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2015个正方形的面积为( )| A. | $5•{(\frac{3}{2})^{2013}}$ | B. | $5•{(\frac{3}{2})^{4026}}$ | C. | $5•{(\frac{3}{2})^{4028}}$ | D. | $5•{(\frac{3}{2})^{4030}}$ |