题目内容
7．已知二次函数y=ax2+bx+c（a≠0）与x轴交于点（x1，0）与（x2，0），其中x1＜x2，方程ax2+bx+c-a=0的两根为m、n（m＜n），则下列判断正确的是（ ）| A． | b2-4ac≥0 | B． | x1+x2＞m+n | C． | m＜n＜x1＜x2 | D． | m＜x1＜x2＜n |
分析 分别画出a＞0和a＜0时二次函数的图象，利用图象选择正确的选项即可．
解答 解：当a＞0时，作图如图1：
b2-4ac＞0，m＜x1＜x2＜n；
当a＜0时，作图如图2，
由图象可知b2-4ac＞0，m＜x1＜x2＜n；
综上可知，D选项m＜x1＜x2＜n正确；
故选D．
点评 本题主要考查了抛物线与x轴的交点的知识，解答本题的关键是正确地作出二次函数的图象，结合图象进行答题，此题有一定的难度．
练习册系列答案
相关题目
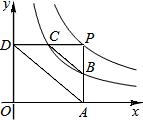如图，点P是反比例函数y=$\frac{6}{x}$（x＞0）的图象上任意一点，PA⊥x轴于A，PD⊥y轴于点D，分别交反比例函数y=$\frac{k}{x}$（x＞0，0＜k＜6）的图象于点B，C．下列结论：
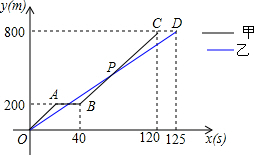在运动会径赛中，甲、乙同时起跑，刚跑出200m，甲不慎摔倒，他又迅速地爬起来继续投入比赛，若他们所跑的路程y（m）与比赛时间x（s）的关系如图，有下列说法：①他们进行的是800m比赛；②乙全程的平均速度为6.4m/s；③甲摔倒之前，乙的速度快；④甲再次投入比赛后的平均速度为7.5m/s；⑤甲再次投入比赛后在距离终点300米时追上了乙．其中正确的个数有（ ）
2．半径为R的圆内接正三角形的面积是（ ）
| A． | $\frac{\sqrt{3}}{2}$R2 | B． | πR2 | C． | $\frac{3\sqrt{3}}{2}$R2 | D． | $\frac{3\sqrt{3}}{4}$R2 |
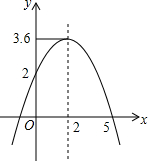二次函数y=ax2+bx+c的图象如图所示．有下列结论：①a-b+c=0；②4a+b=0；③当y=2时，x等于0；④ax2+bx+c=-4有两个不相等的实数根．其中正确的个数是（ ）
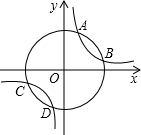如图，以原点为圆心的圆与反比例函数y=$\frac{3}{x}$的图象交于A、B、C、D四点，已知点A的横坐标为1，则点C的横坐标（ ）
△ABC中，点D在边AC上，AB=AC，AD=BD=BC，求出∠A的度数．