题目内容
9.解不等式:|x+2|+|x-3|<7.分析 通过绝对值因式为0,求出x的值,分三个区间讨论:x≤-2,-2<x≤3,x>3,去掉绝对值符号,再根据不等式的性质求出x的取值范围即可.
解答 解:①当x≤-2时,原不等式可化为-x-2-(x-3)<7,
解得,x>-3,结合x≤-2,
故-3<x≤-2是原不等式的解;
②当-2<x≤3时,原不等式可化为x+2-x+3<7,
解得x任意实数,结合-2<x≤3,故-2<x≤3是原不等式的解;
③当x>3时,原不等式化为x+2+x-3<7,
解之得x<4,结合x>3,故3<x<4是原不等式的解.
由①②③可知,-3<x<4,
原不等式的解是-3<x<-4.
点评 本题考查的是带绝对值符号的一元一次不等式的解法,解答此题的关键是熟知绝对值的性质及不等式的基本性质.

练习册系列答案
相关题目
19.分解因式4x2-16y2的结果是( )
| A. | (2x-4y)2 | B. | (2x-4y)(2x+4y) | C. | 4(x2-4y2) | D. | 4(x-2y)(x+2y) |
20.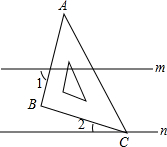 如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )
如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )
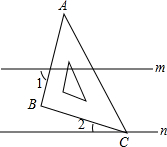 如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )
如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.下列抛物线中,对称轴是x=$\frac{1}{2}$的是( )
| A. | $y=\frac{1}{2}{x^2}$ | B. | y=x2+2x | C. | y=x2+x+2 | D. | y=x2-x-2 |
7.已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m、n(m<n),则下列判断正确的是( )
| A. | b2-4ac≥0 | B. | x1+x2>m+n | C. | m<n<x1<x2 | D. | m<x1<x2<n |
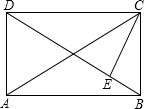 已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.
已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE. 如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?
如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?