题目内容
12.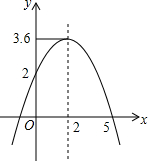 二次函数y=ax2+bx+c的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0;④ax2+bx+c=-4有两个不相等的实数根.其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示.有下列结论:①a-b+c=0;②4a+b=0;③当y=2时,x等于0;④ax2+bx+c=-4有两个不相等的实数根.其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 A:首先根据对称轴是x=2,二次函数y=ax2+bx+c的图象与x轴的一个交点是(5,0),可得二次函数y=ax2+bx+c的图象与x轴的另一个交点是(-1,0),即a-b+c=0,据此判断即可.
B:根据对称轴是x=-$\frac{b}{2a}$=2,可得4a+b=0,据此判断即可.
C:首先判断出二次函数y=ax2+bx+c的图象与y轴的交点是(0,2),然后根据对称轴是x=2,可得当y=2时,x等于0或4,据此判断即可.
D:根据二次函数y=ax2+bx+c的图象的对称性,可得ax2+bx+c=-4有两个不相等的实数根,据此判断即可.
解答 解:∵对称轴是x=2,二次函数y=ax2+bx+c的图象与x轴的一个交点是(5,0),
∴二次函数y=ax2+bx+c的图象与x轴的另一个交点是(-1,0),
即a-b+c=0,
∴结论①正确;
∵x=-$\frac{b}{2a}$=2,
∴4a+b=0,
∴结论②正确;
∵二次函数y=ax2+bx+c的图象与y轴的交点是(0,2),对称轴是x=2,
∴当y=2时,x等于0或4,
∴结论③不正确;
∵ax2+bx+c=-4有两个不相等的实数根,
∴结论④正确.
综上,可得
正确结论的个数是3个:①②④.
故选:C.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
相关题目
20. 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )| A. | 2≤k≤4 | B. | 2≤k≤5 | C. | 2≤k≤8 | D. | 5≤k≤8 |
7.已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m、n(m<n),则下列判断正确的是( )
| A. | b2-4ac≥0 | B. | x1+x2>m+n | C. | m<n<x1<x2 | D. | m<x1<x2<n |
4.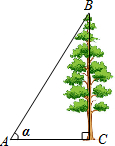 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )| A. | 6sin75°米 | B. | $\frac{6}{cos75°}$米 | C. | $\frac{6}{tan75°}$米 | D. | 6tan75°米 |
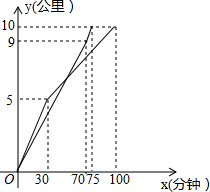 横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是$\frac{1}{6}$公里/分;(2)乙在冲刺阶段的速度$\frac{1}{5}$公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是$\frac{1}{6}$公里/分;(2)乙在冲刺阶段的速度$\frac{1}{5}$公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( ) 如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?
如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?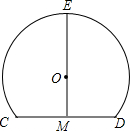 一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )
一个隧道的横截面如图所示,它的形状是以点O为圆心,5为半径的圆的一部分,M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E.若CD=6,则隧道的高(ME的长)为( )