题目内容
16. △ABC中,点D在边AC上,AB=AC,AD=BD=BC,求出∠A的度数.
△ABC中,点D在边AC上,AB=AC,AD=BD=BC,求出∠A的度数.
分析 设∠A=x°,由已知条件开始,通过边相等,得到角相等,再由三角形内角和列出方程进行解答.
解答 解:设∠A=x°.
∵BD=AD,
∴∠A=∠ABD=x°,
∠BDC=∠A+∠ABD=2x°,
∵BD=BC,
∴∠BDC=∠BCD=2x°,
∵AB=AC,
∴∠ABC=∠BCD=2x°,
在△ABC中,
x+2x+2x=180,
解得:x=36,
∴∠A=36°.
点评 此题考查了等腰三角形的性质,关键是设∠A=x°,再根据等腰三角形的性质底角相等和三角形内角和定理得出方程进行解答.

练习册系列答案
相关题目
7.已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m、n(m<n),则下列判断正确的是( )
| A. | b2-4ac≥0 | B. | x1+x2>m+n | C. | m<n<x1<x2 | D. | m<x1<x2<n |
4.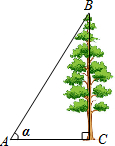 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )| A. | 6sin75°米 | B. | $\frac{6}{cos75°}$米 | C. | $\frac{6}{tan75°}$米 | D. | 6tan75°米 |
5.在菱形ABCD中,如果∠A:∠D=1:5,菱形的高是2cm,那么下列说法中,正确的是( )
| A. | 菱形的周长是8cm | B. | 菱形的面积是4cm2 | ||
| C. | 菱形的周长是10cm | D. | 菱形的面积是8cm2 |
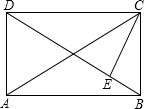 已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.
已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.