题目内容
2.半径为R的圆内接正三角形的面积是( )| A. | $\frac{\sqrt{3}}{2}$R2 | B. | πR2 | C. | $\frac{3\sqrt{3}}{2}$R2 | D. | $\frac{3\sqrt{3}}{4}$R2 |
分析 根据题意画出图形,先求出正三角形的中心角及边心距,再根据三角形的面积公式求解即可.
解答 解: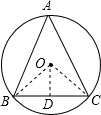 如图所示,过O作OD⊥BC于D;
如图所示,过O作OD⊥BC于D;
∵此三角形是正三角形,
∴∠BOC=$\frac{360°}{3}$=120°.
∵OB=OC,
∴∠BOD=$\frac{1}{2}$×120°=60°,
∴∠OBD=30°;
∵OB=R,
∴OD=$\frac{R}{2}$,BD=OB•cos30°=$\frac{\sqrt{3}R}{2}$,
∴BC=2BD=2×$\frac{\sqrt{3}R}{2}$=$\sqrt{3}$R,
∴S△BOC=$\frac{1}{2}$×BC×OD=$\frac{\sqrt{3}R}{2}$×$\frac{R}{2}$=$\frac{\sqrt{3}{R}^{2}}{4}$,
∴S△ABC=3×$\frac{\sqrt{3}{R}^{2}}{4}$=$\frac{3\sqrt{3}}{4}$R2.
故选D.
点评 本题考查圆的内接正三角形的性质及等边三角形的面积的计算.规律与趋势:圆的内接正三角形的计算是圆中的基本计算,正三角形的相关性质则是解决这类问题的关键.其中,已知边长求面积,已知高求面积等都是常见的计算.

练习册系列答案
相关题目
3.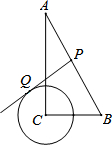 如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )
如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )
 如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )
如图,在Rt△ABC中,∠C=Rt∠,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2-$\frac{\sqrt{3}}{3}$ |
10.下列抛物线中,对称轴是x=$\frac{1}{2}$的是( )
| A. | $y=\frac{1}{2}{x^2}$ | B. | y=x2+2x | C. | y=x2+x+2 | D. | y=x2-x-2 |
7.已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m、n(m<n),则下列判断正确的是( )
| A. | b2-4ac≥0 | B. | x1+x2>m+n | C. | m<n<x1<x2 | D. | m<x1<x2<n |