题目内容
15.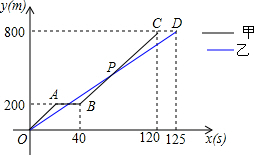 在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( )
在运动会径赛中,甲、乙同时起跑,刚跑出200m,甲不慎摔倒,他又迅速地爬起来继续投入比赛,若他们所跑的路程y(m)与比赛时间x(s)的关系如图,有下列说法:①他们进行的是800m比赛;②乙全程的平均速度为6.4m/s;③甲摔倒之前,乙的速度快;④甲再次投入比赛后的平均速度为7.5m/s;⑤甲再次投入比赛后在距离终点300米时追上了乙.其中正确的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 ①由函数图象可以直接得出比赛的距离;
②由路程÷时间就可以得出速度得出结论;
③由函数图象可以得出相同的时间乙走的路程少,所以乙的速度慢;
④由600÷80就可以求出甲再次投入比赛后的平均速度而得出结论;
⑤由待定系数法分别求出BC和OD的解析式就可以求出结论.
解答 解:①由函数图象,得:甲乙比赛的距离为800米,故正确;
②题意,得
800÷125=6.4m/s,故正确;
③由函数图象,得
甲摔倒之前,甲的速度快.故错误;
④由题意,得
600÷80=7.5m/s,故正确;
⑤设BC的解析式为y=kx+b,OD的解析式为y=k1x,由题意,得
$\left\{\begin{array}{l}{200=40k+b}\\{800=120k+b}\end{array}\right.$,800=125k1.
解得:$\left\{\begin{array}{l}{k=7.5}\\{b=-100}\end{array}\right.$,k1=6.4,
∴y=7.5x-100,y=6.4x,
7.5x-100=6.4x,
解得:x=$\frac{1000}{11}$.
800-6.4×$\frac{1000}{11}$=$\frac{2400}{11}$≠300,故错误.
综上所述,正确的有3个.
故选B.
点评 本题考查了一次函数的图象及性质的运用,行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
10.下列抛物线中,对称轴是x=$\frac{1}{2}$的是( )
| A. | $y=\frac{1}{2}{x^2}$ | B. | y=x2+2x | C. | y=x2+x+2 | D. | y=x2-x-2 |
20. 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数$y=\frac{k}{x}$(x>0)的图象与△线段CB、CA都相交,则k的取值范围是( )| A. | 2≤k≤4 | B. | 2≤k≤5 | C. | 2≤k≤8 | D. | 5≤k≤8 |
7.已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m、n(m<n),则下列判断正确的是( )
| A. | b2-4ac≥0 | B. | x1+x2>m+n | C. | m<n<x1<x2 | D. | m<x1<x2<n |
4.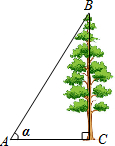 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )| A. | 6sin75°米 | B. | $\frac{6}{cos75°}$米 | C. | $\frac{6}{tan75°}$米 | D. | 6tan75°米 |
5.在菱形ABCD中,如果∠A:∠D=1:5,菱形的高是2cm,那么下列说法中,正确的是( )
| A. | 菱形的周长是8cm | B. | 菱形的面积是4cm2 | ||
| C. | 菱形的周长是10cm | D. | 菱形的面积是8cm2 |

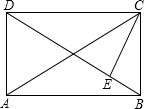 已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE.
已知,如图矩形ABCD,CE⊥BD,∠DCE:∠ECB=3:1,求证:CE=DE. 如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?
如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?