题目内容
17. 纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°.
纸片△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),若∠1=20°,则∠2的度数为60°.
分析 先根据∠A=65°,∠B=75°,求出∠C的度数.再由∠1=20°可求出∠CED的度数,由三角形内角和定理及平角的性质即可求解.
解答 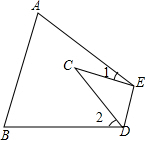 解:∵△ABC中,∠A=65°,∠B=75°,
解:∵△ABC中,∠A=65°,∠B=75°,
∴∠C=180°-∠A-∠B=180°-65°-75°=40°,
∵∠1=20°,
∴∠CED=$\frac{180°-∠1}{2}$=80°,
在△CDE中,∠CDE=180°-∠C-∠CED=180°-40°-80°=60°,
∴∠2=180°-2∠CDE=180°-2×60°=60°,
故答案为60°.
点评 本题考查的是三角形内角和定理及平角的性质,解答此题的关键是熟知三角形的内角和是180°.

练习册系列答案
相关题目
2.若圆的一条弦把圆分成度数比为1:2的两条弧,则优弧所对的圆周角为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
12.一个整式减去a2-b2等于a2+b2,则这个整式为( )
| A. | 2b2 | B. | 2a2 | C. | -2b2 | D. | -2a2 |
2.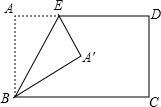 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
 如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )
如图,将矩形ABCD沿BE折叠,点A落在点A′处,若∠CBA′=30°,则∠BEA′等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
7.已知:(-$\sqrt{25}$)2的平方根是a,$\sqrt{{b}^{2}}$=7,且|a+b|=a+b,则a-b的值为( )
| A. | 2或12 | B. | -2或-12 | C. | 2或-12 | D. | -2或12 |
 已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°.
已知,如图,在△ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC外,若∠2=25°,则∠1的度数为105°. 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=15cm2,则S△AOB等于60cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=15cm2,则S△AOB等于60cm2. 四边形ABCD为梯形其中AB∥CD,∠AEG=∠CEH,AF=CF,求证:四边形EGFH为平行四边形.
四边形ABCD为梯形其中AB∥CD,∠AEG=∠CEH,AF=CF,求证:四边形EGFH为平行四边形.