题目内容
12.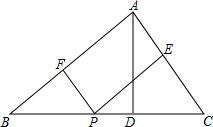 在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.
在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.(1)设BP=x,将S△PEF用x表示;
(2)当P在BC边上什么位置时,S值最大.
分析 (1)首先,求解三角形ABC的面积,然后结合三角形相似,面积比等于相似比的平方,得到△CEP和△BPF的面积,再根据四边形AEPF为平行四边形,从而得到S△PEF的表达式;
(2)根据(1),结合二次函数的性质,求解最大值即可.
解答 解:(1)∵BC=2,BC边上的高AD=1,
∴S△ABC=$\frac{1}{2}$×2×1=1,
∵BP=x,
∴PC=2-x,
∵PE∥AB,
∴△CEP与△CAB相似,
∴$\frac{{S}_{△CEP}}{{S}_{△CAB}}$=($\frac{2-x}{2}$)2,
∴S△CEP=1-x+$\frac{{x}^{2}}{4}$,
同理,得到S△BPF=$\frac{{x}^{2}}{4}$,
∵四边形AEPF为平行四边形,
∴S△PEF=$\frac{1}{2}$S?AEPF=$\frac{1}{2}$(S△ABC-S△CEP-S△BPF)
=-$\frac{1}{4}$x2+$\frac{1}{2}$x(0<x<2).
S△PEF=-$\frac{1}{4}$x2+$\frac{1}{2}$x(0<x<2).
(2)由(1)知S△PEF=-$\frac{1}{4}$x2+$\frac{1}{2}$x=-$\frac{1}{4}$(x-1)2+$\frac{1}{4}$,
∵0<x<2,
∴当x=1时,面积有最大值$\frac{1}{4}$.
点评 本题考查了相似三角形的判定与性质以及建立函数解析式的能力,找准变量之间的关系是解题的关键,属于难题.

练习册系列答案
相关题目
2.下列结论正确的是( )
| A. | 所有直角三角形都相似 | |
| B. | 同弧所对的圆周角相等 | |
| C. | 平分弦的直径垂直弦且平分弦所对的弧 | |
| D. | 当b2-4ac=0时,二次函数y=ax2+bx+c的图象与坐标轴只有一个交点 |
3.2015年“我是歌手”第三季总决赛开赛之前,芒果台娱乐栏目从参加决赛的歌手中选出五位最强人气歌手:孙楠、韩红、黄丽玲、李健、郑淳元,对哪位歌手最有可能获得冠军进行了问卷调查.为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五位歌手中的一位作为调查结果,这样的问卷才能成为有效问卷.从收集到的4800份有效问卷中随机抽取部分问卷进行了统计,绘制了统计图表的一部分如下:
预测最有可能获得冠军歌手的统计表
预测最有可能获得冠军歌手的条形统计图
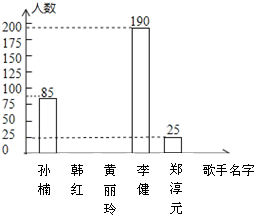
根据统计图表提供的信息,解答下列问题:
(1)a=30%,b=5%;
(2)根据以上信息,请直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测韩红最有可能获得冠军.
预测最有可能获得冠军歌手的统计表
| 歌手名字 | 百分比 |
| 孙楠 | 17% |
| 韩红 | a |
| 黄丽玲 | 10% |
| 李健 | 38% |
| 郑淳元 | b |

根据统计图表提供的信息,解答下列问题:
(1)a=30%,b=5%;
(2)根据以上信息,请直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测韩红最有可能获得冠军.
20.2014年10月16日由科技部、国家知识产权局、国家国防科工局和四川省人民政府主办的第二届中国(绵阳)科技城国际科技博览会(简称“科博会”)在四川绵阳拉开序幕.某部门统计了5天(会前2天和会中3天)的科博会参观人数情况,并作出了如下统计图(表),其中频数分布表和图①表示这5天的日参观人数,图②表示这5天里绵阳本地人的日参观人数情况占参观总人数的百分比折线图.观察统计图(表),解答下列问题:
这5天的日参观人数统计表
(1)这5天时间里的总参观人数;
(2)补全统计表及统计图;
(3)求第4天绵阳本地人的日参观人数;
(4)请写一条从折线图得到的信息.
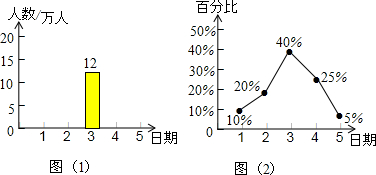
这5天的日参观人数统计表
| 日期 | 频数 | 频率 |
| 1 | 3 | 0.02 |
| 2 | 9 | 0.1 |
| 3 | 12 | 0.4 |
| 4 | 9 | 0.3 |
| 5 | 5.4 | 0.18 |
(2)补全统计表及统计图;
(3)求第4天绵阳本地人的日参观人数;
(4)请写一条从折线图得到的信息.

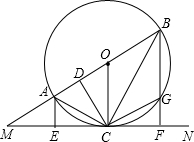 已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG.
已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG.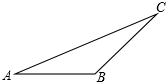 画图并填空:
画图并填空: