题目内容
2.现有2015条直线a1,a2,a3,…,a2015,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2015的位置是垂直.分析 根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答,进而得出规律:a1与其它直线的位置关系为每4个一循环,垂直、垂直、平行、平行,根据此规律即可判断.
解答 解:先判断直线a1与a3的位置关系是:a1⊥a3.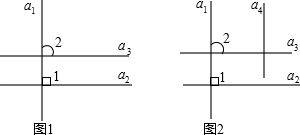
理由如下:如图1,∵a1⊥a2,
∴∠1=90°,
∵a2∥a3,
∴∠2=∠1=90°,
∴a1⊥a3;
再判断直线a1与a4的位置关系是:a1∥a4,如图2;
∵直线a1与a3的位置关系是:a1⊥a3,
直线a1与a4的位置关系是:a1∥a4,
∵2015÷4=503…3,
∴直线a1与a2015的位置关系是:垂直.
故答案为:垂直.
点评 本题考查了平行公理的推导,作出图形更有利于规律的发现以及规律的推导,解题的关键是:结合图形先判断几组直线的关系,然后找出规律.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14.下列运算正确的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | 2(2a-b)=4a-b | C. | 2a+3b=5ab | D. | (a+b)2=a2+b2 |
11.二元一次方程2x+y=7的正整数解有多少组( )
| A. | 2 | B. | 3 | C. | 5 | D. | 4 |
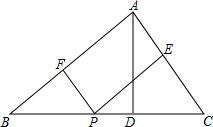 在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.
在△ABC中,BC=2,BC边上的高AD=1,P是BC上任一点,PE∥AB交AC于E,PF∥AC交AB于F.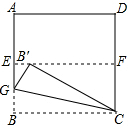 如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展开,然后沿直线CG折叠,使B点落在EF上,对应点为B′
如图,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展开,然后沿直线CG折叠,使B点落在EF上,对应点为B′ 如图,在平面直角坐标系中:
如图,在平面直角坐标系中: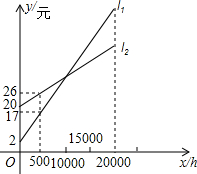 如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,
如图,L1,L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图象,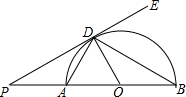 如图,AB是半圆的直径,O为圆心,AD、AB是半圆的弦,点D是⊙O的切点.
如图,AB是半圆的直径,O为圆心,AD、AB是半圆的弦,点D是⊙O的切点.