题目内容
1.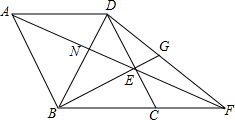 如图,在菱形ABCD中,∠ABC=120°,点E在边CD上(DE>CE),连结AE并延长交BC的延长线于点F,连结DF,连结BE并延长交DF于点G.若BE:EG=49:15,CF=6,则线段DN的长为$\frac{50}{13}$.
如图,在菱形ABCD中,∠ABC=120°,点E在边CD上(DE>CE),连结AE并延长交BC的延长线于点F,连结DF,连结BE并延长交DF于点G.若BE:EG=49:15,CF=6,则线段DN的长为$\frac{50}{13}$.
分析 过点G作GH∥CD交BF于H,如图,利用CE∥GH得到BC:CH=BE:EG=49:15,则设BC=49x,CH=15x,则FH=CF-CH=6-15x,再证明△BCE∽△BHG,利用相似比得到GH=$\frac{64}{49}$EC,接着证明△FGH∽△FDC,利用相似比得到GH=49x•$\frac{6-15x}{6}$,则EC=$\frac{4{9}^{2}x(2-5x)}{3×64}$,然后利用AD∥CF,根据平行线分线段成比例定理得到CE=$\frac{6•49x}{49x+6}$,于是可建立方程$\frac{4{9}^{2}x(2-5x)}{3×64}$=$\frac{6•49x}{49x+6}$,整理得5×(49x)2-68×49x+180=0,设t=49x,则5t2-68t+180=0,解得t1=$\frac{18}{5}$,t2=10,接着利用DE>CE得到t=10,最后利用AD∥BF,根据平行线分线段长比例定理可求出DN的长.
解答 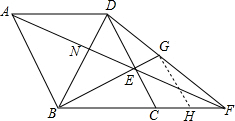 解:过点G作GH∥CD交BF于H,如图,
解:过点G作GH∥CD交BF于H,如图,
∵在菱形ABCD中,∠ABC=120°,
∴AB=AD=BC=CD=BD,
∵CE∥GH,
∴BC:CH=BE:EG=49:15,
设BC=49x,CH=15x,则FH=CF-CH=6-15x,
∵CE∥GH,
∴△BCE∽△BHG,
∴$\frac{CE}{GH}$=$\frac{BE}{BG}$=$\frac{49}{64}$,即GH=$\frac{64}{49}$EC,
∵GH∥CD,
∴△FGH∽△FDC,
∴$\frac{GH}{CD}$=$\frac{HF}{FC}$,即$\frac{GH}{49x}$=$\frac{6-15x}{6}$,
∴GH=49x•$\frac{6-15x}{6}$,
∴$\frac{64}{49}$x•EC=49x•$\frac{6-15x}{6}$,
∴EC=$\frac{4{9}^{2}x(2-5x)}{3×64}$,
∵AD∥CF,
∴$\frac{DE}{CE}$=$\frac{AD}{CF}$,即$\frac{49x-CE}{CE}$=$\frac{49x}{6}$,解得CE=$\frac{6•49x}{49x+6}$,
∴$\frac{4{9}^{2}x(2-5x)}{3×64}$=$\frac{6•49x}{49x+6}$,
整理得5×(49x)2-68×49x+180=0,
设t=49x,
则5t2-68t+180=0,
解得t1=$\frac{18}{5}$,t2=10,
∵DE>CE,
∴AD>CF,
∴t=10,
即AD=BD=BC=10,
∵AD∥BF,
∴$\frac{DN}{BN}$=$\frac{AD}{BF}$=$\frac{10}{10+6}$=$\frac{5}{8}$,
∴DN=$\frac{5}{13}$BD=$\frac{50}{13}$.
故答案为$\frac{50}{13}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了菱形的性质.解决本题的关键是求出菱形的边长.

 名校课堂系列答案
名校课堂系列答案 如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D,
如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D,
 如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路两旁的村庄.
如图,一辆汽车在直线形公路AB上由A向B行驶,M、N是分别位于公路两旁的村庄. 如图,∠AOB=45°,P是∠AOB内一点,PO=5,Q、R分别是OA、OB上的动点,求△PQR周长的最小值5$\sqrt{2}$.
如图,∠AOB=45°,P是∠AOB内一点,PO=5,Q、R分别是OA、OB上的动点,求△PQR周长的最小值5$\sqrt{2}$.