题目内容
9．化简（1）（$\frac{3x}{x-2}$-$\frac{x}{x+2}$）•$\frac{{x}^{2}-4}{x}$
（2）$\frac{x-4}{x-2}$+$\frac{4}{{x}^{2}-4x+4}$÷$\frac{x}{x-2}$．
分析 （1）原式括号中两项通分并利用同分母分式的减法法则计算，约分即可得到结果；
（2）原式第二项利用除法法则变形，约分后通分并利用同分母分式的加法法则计算即可得到结果．
解答 解：（1）原式=$\frac{3{x}^{2}+6x-{x}^{2}+2x}{（x+2）（x-2）}$•$\frac{（x+2）（x-2）}{x}$=2x+8；
（2）原式=$\frac{x-4}{x-2}$+$\frac{4}{（x-2）^{2}}$•$\frac{x-2}{x}$=$\frac{x（x-4）}{x（x-2）}$+$\frac{4}{x（x-2）}$=$\frac{（x-2）^{2}}{x（x-2）}$=$\frac{x-2}{x}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
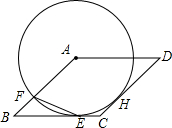如图，⊙A与菱形ABCD的边BC相切于点E，与边AB相交于点F，连结EF
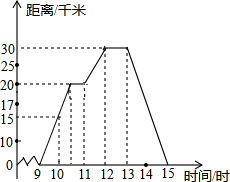小樱某天上午9时骑自行车离开家，下午15时回到家，如图所示是小樱离家的距离与时间的变化图象．
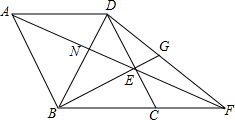如图，在菱形ABCD中，∠ABC=120°，点E在边CD上（DE＞CE），连结AE并延长交BC的延长线于点F，连结DF，连结BE并延长交DF于点G．若BE：EG=49：15，CF=6，则线段DN的长为$\frac{50}{13}$．
18．有40个数据，共分成6组，第1-4组的频数分别是10、5、7、6．第5组的占10%，则第6组占（ ）
| A． | 25% | B． | 30% | C． | 15% | D． | 20% |
19．表给出了y=x2+bx+c中x与y的一些对应值：
（1）设y=x2+bx+c，求b和c的值；并在表内的空格中填入适当的数；
（2）将抛物线y=x2+bx+c做怎样的平移，使它的顶点为坐标原点？
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
（2）将抛物线y=x2+bx+c做怎样的平移，使它的顶点为坐标原点？