题目内容
12.x取什么值时,分式$\frac{{x}^{2}-2x-3}{{x}^{2}+2x}$的值是零?是正数?是负数?分析 分式值为零的条件是分子等于零且分母不等于零;分子和分母同号时值为正数;分子和分母异号时值为负数.
解答 解:∵分式$\frac{{x}^{2}-2x-3}{{x}^{2}+2x}$的值为零,
∴x2-2x-3=0,且x2+2x≠0.
解得:x=3或x=-1.
$\frac{{x}^{2}-2x-3}{{x}^{2}+2x}$=$\frac{(x-3)(x+1)}{x(x+2)}$.
①当x<-2时,x(x+1)(x+2)(x-3)>0,分式的值为正数;
②当-2<x<-1时,x(x+1)(x+2)(x-3)<0,分式的值为负数;
③当-1<x<0时,x(x+1)(x+2)(x-3)>0,分式的值为正数;
④当0<x<3时,x(x+1)(x+2)(x-3)<0,分式的值为负数;
⑤当x>3时,x(x+1)(x+2)(x-3)>0,分式的值为正数;
综上所述当x<-2或-1<x<0,或x>3时,分式的值为正数;当-2<x<-1或0<x<3时,分式的值为负数.
点评 本题主要考查的是分式的值,依据分类讨论思想求得分式的值为正数和负数时x的取值范围是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交AC于点D,若BC=4,CD=2,则⊙O的半径的值是$\frac{4}{3}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交AC于点D,若BC=4,CD=2,则⊙O的半径的值是$\frac{4}{3}$. 如图,△ABC绕点C旋转后,顶点A旋转到了点D.
如图,△ABC绕点C旋转后,顶点A旋转到了点D.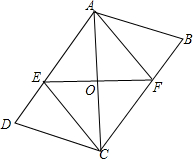 如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.
如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.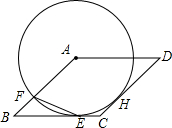 如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF
如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF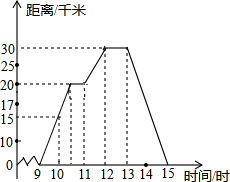 小樱某天上午9时骑自行车离开家,下午15时回到家,如图所示是小樱离家的距离与时间的变化图象.
小樱某天上午9时骑自行车离开家,下午15时回到家,如图所示是小樱离家的距离与时间的变化图象.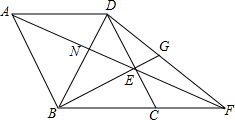 如图,在菱形ABCD中,∠ABC=120°,点E在边CD上(DE>CE),连结AE并延长交BC的延长线于点F,连结DF,连结BE并延长交DF于点G.若BE:EG=49:15,CF=6,则线段DN的长为$\frac{50}{13}$.
如图,在菱形ABCD中,∠ABC=120°,点E在边CD上(DE>CE),连结AE并延长交BC的延长线于点F,连结DF,连结BE并延长交DF于点G.若BE:EG=49:15,CF=6,则线段DN的长为$\frac{50}{13}$.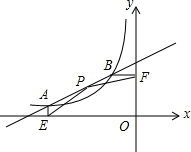 如图,函数y=$\frac{k}{x}$(x<0)的图象与直线y=$\frac{1}{2}$x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=-$\frac{5}{2}$,xA-xB=-3,则k的值是( )
如图,函数y=$\frac{k}{x}$(x<0)的图象与直线y=$\frac{1}{2}$x+m相交于点A和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且xP=-$\frac{5}{2}$,xA-xB=-3,则k的值是( )