在坐标系中.以原点为圆心.以5个单位长度为半径.点P的坐标为A．圆O内B．圆O外C．圆O上D．不确定题目和参考答案——青夏教育精英家教网—

题目内容

13．在坐标系中，以原点为圆心，以5个单位长度为半径，点P的坐标为（4，2），则点P在（　　）

A．

圆O内

B．

圆O外

C．

圆O上

D．

不确定

分析要确定点与圆的位置关系，主要确定点与圆心的距离与半径的大小关系；本题可由勾股定理算出点与圆心的距离d，则d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．

解答解：∵点P的坐标为（4，2），
∴OP=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$＜5，
∴点P在⊙C内．
故选A．

点评本题考查了对点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．

练习册系列答案

4．下列函数中：①y=1-2x²；②y=$\frac{1}{{x}^{2}}$；③y=x（1-x）；④y=（1-2x）（1+3x），是二次函数的有（　　）

1．若二次函数y=ax²+bx+c的图象经过原点和第一、二、四象限，那么a＞0，b＜00，c=0（填“＞”，“＜”或“=”）

8．若|a-3|与（b+2）²互为相反数，则代数式2a²b的值为-36．

18．设a=$\sqrt{2012}$+$\sqrt{2008}$，b=$\sqrt{2013}$+$\sqrt{2007}$，c=$\sqrt{2014}$+$\sqrt{2006}$，则a，b，c之间的大小关系是（　　）

5．若A（2，m）和点B（-1，n）都在抛物线y=x²上，则点（m-3n，-1）在抛物线y=-x²上（填“在”或“不在”）

2．

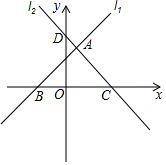如图所示，在平面直角坐标系中，直线l₁：y=x+1与l₂：y=-x+2分别交x轴于点B和点C，点D是直线l₂与y轴的交点，两直线交于点A．
（1）求点A的坐标；
（2）设M（x，y）是直线l₁上一点．△BCM的面积为S．求S与x的函数关系式；并探究当点M运动到什么位置时，△BCM的面积为6．
（3）直线1₁上是否存在点P，使△OBP为等腰三角形，如果存在，直接写出P点的坐标；如果不存在，请说明理由．
（4）过点A作x轴的垂线1₃，在1₃上是否存在一点Q，使得△BDQ的周长最小？若存在，请求出点Q的坐标和周长的最小值；若不存在，请说明理由．

5．

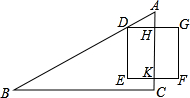在《九章算术》“勾股”章中有这样一个问题：“今有邑方不知大小，各中开门，出北门二十步有木，出南门十回步，折而西行一千七百七十五步见木，问邑方几何．”用今天的话说，大意是：如图，DEFG是一座正方形小城，北门H位于DG的中点，南门K位于EF的中点，出北门20步到A处有一树木，出南门14步到C，向西行1775步到B处正好看到A处的树木（即点D在直线AB上），小城的边长为多少步，若设小城的边长为2x 步，则可列方程为$\frac{20}{20+14+2x}$=$\frac{x}{1775}$．

试题分类