题目内容
1.若二次函数y=ax2+bx+c的图象经过原点和第一、二、四象限,那么a>0,b<00,c=0(填“>”,“<”或“=”)分析 由抛物线y=ax2+bx+c经过原点和第一、二、四象限得c=0,抛物线开口向上,对称轴在y轴的右侧,则a>0,x=-$\frac{b}{2a}$>0,即可得到b<0.
解答  解:如图,
解:如图,
∵抛物线y=ax2+bx+c经过原点,
∴c=0,
∵抛物线y=ax2+bx+c经过第一、二、四象限,
∴抛物线开口向上,对称轴在y轴的右侧,
∴a>0,x=-$\frac{b}{2a}$>0,
∴b<0.
故答案为>,<,=.
点评 本题考查了二次函数y=ax2+bx+c(a≠0)的图象与系数的关系:a>0,开口向上;a<0,开口向下;对称轴为直线x=-$\frac{b}{2a}$,a与b同号,对称轴在y轴的左侧,a与b异号,对称轴在y轴的右侧;当c>0,抛物线与y轴的交点在x轴的上方,c=0,抛物线经过原点,c<0,抛物线与y轴的交点在x轴的下方;抛物线的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在坐标系中,以原点为圆心,以5个单位长度为半径,点P的坐标为(4,2),则点P在( )
| A. | 圆O内 | B. | 圆O外 | C. | 圆O上 | D. | 不确定 |
10.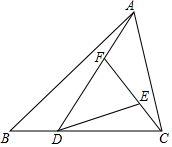 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{13}{18}$ | D. | $\frac{8}{27}$ |
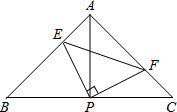 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论: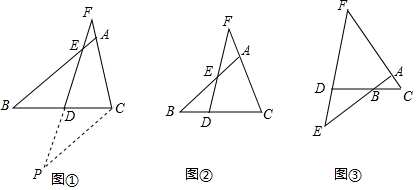
 根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.
根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.