题目内容
2.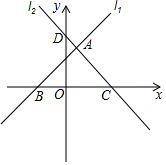 如图所示,在平面直角坐标系中,直线l1:y=x+1与l2:y=-x+2分别交x轴于点B和点C,点D是直线l2与y轴的交点,两直线交于点A.
如图所示,在平面直角坐标系中,直线l1:y=x+1与l2:y=-x+2分别交x轴于点B和点C,点D是直线l2与y轴的交点,两直线交于点A.(1)求点A的坐标;
(2)设M(x,y)是直线l1上一点.△BCM的面积为S.求S与x的函数关系式;并探究当点M运动到什么位置时,△BCM的面积为6.
(3)直线11上是否存在点P,使△OBP为等腰三角形,如果存在,直接写出P点的坐标;如果不存在,请说明理由.
(4)过点A作x轴的垂线13,在13上是否存在一点Q,使得△BDQ的周长最小?若存在,请求出点Q的坐标和周长的最小值;若不存在,请说明理由.
分析 (1)解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-x+2}\end{array}\right.$,即可解决问题.
(2)如图1中,作AQ⊥BC于Q.分两种情形求解①当x≥-1时,BM=$\sqrt{2}$(x+1),S=$\frac{1}{2}$•BM•AC=$\frac{1}{2}$×$\sqrt{2}$(x+1)×$\frac{3}{2}$$\sqrt{2}$=$\frac{3}{2}$x+$\frac{3}{2}$,②当x<-1时,BM=$\sqrt{2}$(1-x),S=$\frac{1}{2}$•BM•AC=$\frac{1}{2}$×$\sqrt{2}$(1-x)×$\frac{3}{2}$$\sqrt{2}$=$\frac{3}{2}$-$\frac{3}{2}$x.
(3)如图2中,分三种情形①当OB=OP1时,P1在y轴上,②BP=BO时,③当P4B=P4O时,P4在OB的垂直平分线上,分别求解即可.
(4)如图3中,连接BD.由题意D(0,2),C(2,0),B(-1,0),可得BD=$\sqrt{5}$,DC=2$\sqrt{2}$,因为B、C关于直线l3对称,所以当点Q与A重合时,QD+QB最短,即△QBD的周长最短,由此即可解决问题.
解答 解:(1)由$\left\{\begin{array}{l}{y=x+1}\\{y=-x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
∴点A坐标为($\frac{1}{2}$,$\frac{3}{2}$).
(2)如图1中,作AQ⊥BC于Q.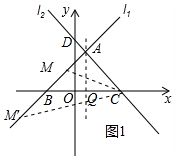
∵B(-1,0),C(2,0),A($\frac{1}{2}$,$\frac{3}{2}$),
∴AQ=BQ=QC=$\frac{3}{2}$,
∴∠BAC=90°,AB=AC=$\frac{3}{2}$$\sqrt{2}$,
①当x≥-1时,BM=$\sqrt{2}$(x+1),
∴S=$\frac{1}{2}$•BM•AC=$\frac{1}{2}$×$\sqrt{2}$(x+1)×$\frac{3}{2}$$\sqrt{2}$=$\frac{3}{2}$x+$\frac{3}{2}$.
②当x<-1时,BM=$\sqrt{2}$(1-x),
S=$\frac{1}{2}$•BM•AC=$\frac{1}{2}$×$\sqrt{2}$(1-x)×$\frac{3}{2}$$\sqrt{2}$=$\frac{3}{2}$-$\frac{3}{2}$x
综上所述,S=$\left\{\begin{array}{l}{\frac{3}{2}x+\frac{3}{2}}&{(x≥-1)}\\{\frac{3}{2}-\frac{3}{2}x}&{(x<-1)}\end{array}\right.$.
当S=6时,$\frac{3}{2}$x+$\frac{3}{2}$=6或$\frac{3}{2}$-$\frac{3}{2}\\;x$x=6,
解得x=3或-3.
此时M(3,4)或(-3,-2).
(3)如图2中,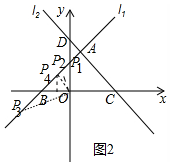
①当OB=OP1时,P1在y轴上,坐标为(0,1).
②BP=BO时,可得P2($\frac{\sqrt{2}}{2}$-1,$\frac{\sqrt{2}}{2}$),P3(-1-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
③当P4B=P4O时,P4在OB的垂直平分线上,P4(-$\frac{1}{2}$,$\frac{1}{2}$).
综上所述,当△OBP为等腰三角形时,点P坐标为(0,1)或($\frac{\sqrt{2}}{2}$-1,$\frac{\sqrt{2}}{2}$)或(-1-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\frac{1}{2}$,$\frac{1}{2}$).
(4)如图3中,连接BD.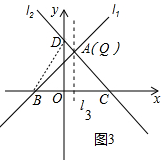
由题意D(0,2),C(2,0),B(-1,0),
∴BD=$\sqrt{5}$,DC=2$\sqrt{2}$,
∵B、C关于直线l3对称,
∴当点Q与A重合时,QD+QB最短,即△QBD的周长最短,
△QBD的周长的最小值为BD+AD+AB=BD+DA+AC=BD+DC=$\sqrt{5}$+2$\sqrt{2}$.
点评 本题考查一次函数综合题、三角形的面积、等腰三角形的性质和判定、最短问题等知识,解题的关键是灵活应用所学知识解决问题,学会用分类讨论的思想思考问题,学会利用对称解决最值问题,属于中考压轴题.

| A. | 圆O内 | B. | 圆O外 | C. | 圆O上 | D. | 不确定 |
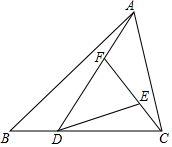 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{13}{18}$ | D. | $\frac{8}{27}$ |
| A. | 2$\sqrt{5}$ | B. | -2$\sqrt{5}$ | C. | -10 | D. | 10 |
| A. | y=$\frac{1}{x}$ | B. | y=-$\frac{1}{x}$ | C. | y=$\frac{5}{x}$ | D. | y=-$\frac{5}{x}$ |
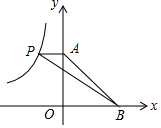 如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.
如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$. 根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.
根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.