题目内容
5.若A(2,m)和点B(-1,n)都在抛物线y=x2上,则点(m-3n,-1)在抛物线y=-x2上(填“在”或“不在”)分析 将A(2,m)和点B(-1,n)分别代入y=x2,可求得m,n的值,再判断点(m-3n,-1)是否在抛物线y=-x2上.
解答 解:把A(2,m)和点B(-1,n)分别代入y=x2,
得m=4,n=1,
∴点(m-3n,-1)的坐标(1,-1),
当x=1时,y=-1,
∴点(1,-1)在抛物线y=-x2上,
故答案为:在.
点评 本题考查了函数图象上的点的坐标与函数解析式的关系,将方程转化为关于未知系数的方程.结合图形更易解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.在坐标系中,以原点为圆心,以5个单位长度为半径,点P的坐标为(4,2),则点P在( )
| A. | 圆O内 | B. | 圆O外 | C. | 圆O上 | D. | 不确定 |
20.若方程3x=bx+4(b是已知数)是一元一次方程,则( )
| A. | b≠0 | B. | b≠3 | C. | b=-3 | D. | b为任意数 |
10.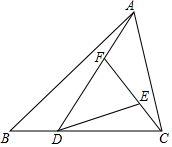 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{13}{18}$ | D. | $\frac{8}{27}$ |
17.化简$\sqrt{5×(-2)^{2}}$,结果是 ( )
| A. | 2$\sqrt{5}$ | B. | -2$\sqrt{5}$ | C. | -10 | D. | 10 |
17.下列等式中不一定成立的是( )
| A. | $\frac{y}{x}=\frac{xy}{x^2}$ | B. | $\frac{y}{x}=\frac{πy}{πx}$ | C. | $\frac{y}{x}=\frac{yz}{xz}$ | D. | $\frac{y}{x}=\frac{{y({{x^2}+2})}}{{x({{x^2}+2})}}$ |
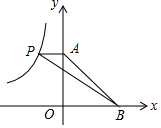 如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.
如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.