题目内容

6．二次函数y=x2-2x-3的图象绕点（1，0）旋转180°的图象的解析式是y=-（x-1）2+4．

分析 由于图象绕定点旋转180°，得到顶点坐标改变，而抛物线开口方向相反，然后根据顶点式写出解析式．

解答 解：∵抛物线y=x2-2x-3=（x-1）2-4的顶点坐标为（1，-4），
∴绕（1，0）旋转180°后的抛物线的顶点坐标为（1，4），
∴所得到的图象的解析式为y=-（x-1）2+4．
故答案为：y=-（x-1）2+4

点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．

练习册系列答案
相关题目
16．把下列各数分别填入相应的集合里.$-4，-|{-\frac{4}{3}}|，0，\frac{22}{7}，\frac{π}{2}，2015，-（+5），0.01001…，-2.333…，300%$
（1）正数集合：{                                                 …}；
（2）负数集合：{                                                 …}；
（3）整数集合：{                                                 …}；
（4）无理数集合：{                                               …}．
17．若点C是线段AB的黄金分割点（AC＜BC），则$\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$．
14．某种商品每天的销售利润y（元）与销售单价x（元）之间满足关系：y=-x2+20x-75，则销售单价为10元时，该种商品每天的销售利润最大为25元．
1．抛物线y=ax2+bx+c经过点A（-3，0），对称轴是直线x=-1，则a+3+c=3．
11．若a＜0，b＞0，且|a|＜|b|，则下列整式的值中为负数的是（　　）
A．a+bB．a-bC．b-aD．|a-b|
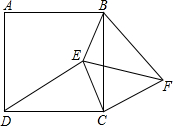4．如图，四边形ABCD是正方形，E是正方形ABCD内一点，F是正方形ABCD外一点，连结BE、CE、DE、BF、CF、EF．
（1）若∠EDC=∠FBC，ED=FB，试判断△ECF的形状，并说明理由．
（2）在（1）的条件下，当BE：CE=1：2，∠BEC=135°时，求BE：BF的值．
（3）在（2）的条件下，若正方形ABCD的边长为（3$\sqrt{3}$+$\sqrt{7}$）cm，∠EDC=30°，求△BCF的面积．
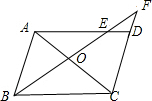1．平行四边形ABCD中，过B作直线交AC、AD于O、E，交CD的延长线于F，求证：
（1）AE：AD=CD：CF；
（2）OB2=OE：OF；
（3）OA2：OC2=OE：OF．
2．在规定向右为正方向的数轴上从左至右依次有A、B、C、D四点，线段AB=2（单位长度），CD=4（单位长度），点A在数轴上表示的数是-10，点C在数轴上表示的数是16，若线段AB以6个单位长度/秒的速度向右匀速运动，同时线段CD以2个单位长度/秒的速度向左匀速运动．
（1）在B点C点重合前，运动多少秒时BC=8（单位长度）？此时点B在数轴上表示的数是多少？
（2）若P是线段AB上一点，当B点与C点重合时，是否存在关系式$\frac{BD-AP}{PC}$=3？若存在，求线段PC的长；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网