题目内容
1.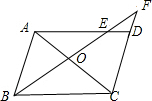 平行四边形ABCD中,过B作直线交AC、AD于O、E,交CD的延长线于F,求证:
平行四边形ABCD中,过B作直线交AC、AD于O、E,交CD的延长线于F,求证:(1)AE:AD=CD:CF;
(2)OB2=OE:OF;
(3)OA2:OC2=OE:OF.
分析 (1)在?ABCD中,根据AB∥CD,AD∥BC,AD=BC,AB=CD,于是得到△AOB∽△COF,△AOE∽△BOC,推出AE:BC=AO:OC,AB:CF=AO:OC,等量代换得到AE:AD=CD:CF;
(2)在?ABCD中,根据AB∥CD,AD∥BC,于是得到△AOB∽△COF,△AOE∽△BOC,根据相似三角形的性质得到OE:BO=AO:OC,OB:OF=AO:OC,等量代换得到OB:OF=OE:OB,于是得结论;
(3)由(2)证得OE:BO=AO:OC,OB:OF=AO:OC,两式相乘即可得到结论.
解答 证明:(1)在?ABCD中,∵AB∥CD,AD∥BC,AD=BC,AB=CD,
∴△AOB∽△COF,△AOE∽△BOC,
∴AE:BC=AO:OC,AB:CF=AO:OC,
∴AE:AD=CD:CF;
(2)在?ABCD中,∵AB∥CD,AD∥BC,
∴△AOB∽△COF,△AOE∽△BOC,
∴OE:BO=AO:OC,OB:OF=AO:OC,
∴OB:OF=OE:OB,
即OB2=OF•OE;
(3)由(2)证得OE:BO=AO:OC,OB:OF=AO:OC,
∴$\frac{OA}{OC}•\frac{OA}{OC}=\frac{OE}{OB}•\frac{OB}{OF}$,
∴OA2:OC2=OE:OF.
点评 此题考查了相似三角形的判定和性质,证线段的乘积相等,通常转化为比例式形式,再证明所在的三角形相似,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
9.若(3x3+M)(2x2-1)是一个五次多项式,则下列说法中正确的是( )
| A. | M是一个三次单项式 | B. | M是一个三次多项式 | ||
| C. | M的次数不高于三 | D. | M不可能是一个常数 |
11.下列叙述正确的是( )
| A. | 整数包括正整数和负整数 | B. | 正分数和负分数统称为分数 | ||
| C. | 一个有理数不是正整数就是负数 | D. | 零是整数但不是自然数 |
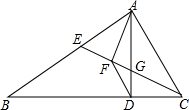 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD⊥CE于G点,求证:∠B=∠CFD.
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD⊥CE于G点,求证:∠B=∠CFD.