题目内容
4.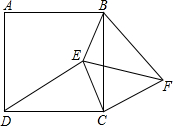 如图,四边形ABCD是正方形,E是正方形ABCD内一点,F是正方形ABCD外一点,连结BE、CE、DE、BF、CF、EF.
如图,四边形ABCD是正方形,E是正方形ABCD内一点,F是正方形ABCD外一点,连结BE、CE、DE、BF、CF、EF.(1)若∠EDC=∠FBC,ED=FB,试判断△ECF的形状,并说明理由.
(2)在(1)的条件下,当BE:CE=1:2,∠BEC=135°时,求BE:BF的值.
(3)在(2)的条件下,若正方形ABCD的边长为(3$\sqrt{3}$+$\sqrt{7}$)cm,∠EDC=30°,求△BCF的面积.
分析 (1)利用正方形的性质结合全等三角形的判定与性质得出△BCF≌△DCE(ASA),进而得出△ECF是等腰直角三角形;
(2)利用已知条件得出∠BEF=90°,进而利用勾股定理表示出BF的长,进而得出BE:BF的值;
(3)利用(1)(2)中所求得出作FM⊥BC垂足为M,进而表示出BM,MC的长,再利用已知正方形的边长得出FM的长,进而得出答案.
解答 (1)证明:在正方形ABCD中,CD=CB,∠DCE+∠BE=∠BCD=90°,
∵EC⊥CF,
∴∠BCF+∠BCE=90°,
∴∠BCF=∠DCE,
在△BCF和△DCE中$\left\{\begin{array}{l}{∠EDC=∠FBC}\\{CD=CB}\\{∠BCF=∠DCE}\end{array}\right.$,
∴△BCF≌△DCE(ASA),
∴EC=FC,
∴∠ECD=∠BCF,
∵∠DCE+∠BCE=90°,
∴∠ECF=90°,
∴△ECF是等腰直角三角形;
(2)解:∵BE:CE=1:2,
∴设BE=a,CE=2a,
∵△ECF是等腰直角三角形,
∴EF=2$\sqrt{2}$a,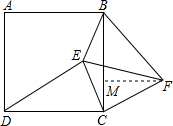
∵∠BEC=135°,∠CEF=45°,
∴∠BEF=90°,
∴BF=$\sqrt{B{E}^{2}+E{F}^{2}}$=3a,
∴BE:BF=1:3;
(3)解:如图所示:作FM⊥BC垂足为M,设BF=3b,FC=2b,
∵∠EDC=30°,∴∠CBF=30°,
在Rt△BFM中,
∴MB=$\frac{\sqrt{3}}{2}$×3b=$\frac{3\sqrt{3}}{2}$b,MF=$\frac{3}{2}$b,
∴MC=$\sqrt{F{C}^{2}-M{F}^{2}}$=$\frac{\sqrt{7}}{2}$b,
∴$\frac{3\sqrt{3}}{2}$b+$\frac{\sqrt{7}}{2}$b=3$\sqrt{3}$$+\sqrt{7}$,
∴b=2,则FM=$\frac{3}{2}$×2=3,
∴△BCF的面积是:$\frac{1}{2}$×BC×FM=$\frac{1}{2}$×(3$\sqrt{3}$+$\sqrt{7}$)×3=$\frac{9\sqrt{3}}{2}$+$\frac{3\sqrt{7}}{2}$.
点评 此题主要考查了全等三角形的判定与性质以及勾股定理和正方形的性质、锐角三角函数关系等知识,正确利用锐角三角函数关系表示出各边长是解题关键.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案| A. | 9 | B. | 10 | C. | 8 | D. | 无法确定 |
| A. | M是一个三次单项式 | B. | M是一个三次多项式 | ||
| C. | M的次数不高于三 | D. | M不可能是一个常数 |
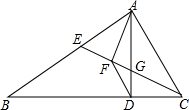 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD⊥CE于G点,求证:∠B=∠CFD.
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD⊥CE于G点,求证:∠B=∠CFD.