题目内容
1．
如图，所示是二次函数y=ax2+bx+c图象的一部分，图象过点A（5，0），对称轴为直线x=1，下列结论中错误的是（ ）| A． | abc＞0 | B． | 当x＜1时，y随x的增大而增大 | ||
| C． | a+b+c＞0 | D． | 方程ax2+bx+c=0的根为x1=-3，x2=5 |
分析 利用抛物线开口方向、抛物线的对称轴位置和抛物线与y轴的交点位置可判断a、b、c的符号，于是可对A选项进行判断；根据二次函数的性质可对B选项进行判断；利用自变量为1时函数值为正可对C选项进行判断；利用抛物线的对称性可得到抛物线与x轴的另一个交点坐标为（-3，0），然后利用抛物线与x轴的交点问题可对D选项进行判断．
解答 解：A、抛物线开口向下得a＜0，抛物线的对称轴在y轴右侧得b＞0，抛物线与y轴的交点在x轴上方得c＞0，则abc＜0，所以A选项的结论错误；
B、a＜0，当x＜1时，y随x的增大而增大，所以B选项的结论正确；
C、当x=1时，y＞0，即a+b+c=0，所以C选项的结论正确；
D、点（5，0）关于直线x=1的对称点为（-3，0），所以方程ax2+bx+c=0的根为x1=-3，x2=5，所以D选项的结论正确．
故选A．
点评 本题考查了二次函数图象与系数的关系：二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．判断D选项的关键是利用抛物线的对称性确定抛物线与x轴的另一个交点．
练习册系列答案
相关题目
9．
如图，AB∥CD，以点A为圆心，小于AC长为半径画圆弧，分别交AB、AC于E、F两点：再分别以E、F为圆心，大于$\frac{1}{2}$EF长为半径画圆弧，两弧交于点G，作射线AG交CD于点H．若∠C=150°，则∠AHC大小是（ ）
如图，AB∥CD，以点A为圆心，小于AC长为半径画圆弧，分别交AB、AC于E、F两点：再分别以E、F为圆心，大于$\frac{1}{2}$EF长为半径画圆弧，两弧交于点G，作射线AG交CD于点H．若∠C=150°，则∠AHC大小是（ ）| A． | 15° | B． | 25° | C． | 30° | D． | 35° |
一次函数y=-3x+b和y=kx+1的图象如图所示，其交点为P（3，4），则不等式（3+k）x≥b-1的解集在数轴上表示正确的是（ ）
6．
如图，在正方形ABCD中，AB=2，延长AB至点E，使得BE=1，EF⊥AE，EF=AE．分别连接AF，CF，M为CF的中点，则AM的长为（ ）
如图，在正方形ABCD中，AB=2，延长AB至点E，使得BE=1，EF⊥AE，EF=AE．分别连接AF，CF，M为CF的中点，则AM的长为（ ）| A． | 2$\sqrt{2}$ | B． | 3$\sqrt{2}$ | C． | $\frac{11}{4}$ | D． | $\frac{\sqrt{26}}{2}$ |
13．
二次函数y=ax2+bx+c（a≠0）图象如图所示，则下列结论中错误的是（ ）
二次函数y=ax2+bx+c（a≠0）图象如图所示，则下列结论中错误的是（ ）| A． | 当m≠1时，a+b＞am2+bm | |
| B． | 若a${x}_{1}^{2}$+bx1=a${x}_{2}^{2}$+bx2，且x1≠x2，则x1+x2=2 | |
| C． | a-b+c＞0 | |
| D． | abc＜0 |
10．在Rt△ABC中∠A=90°，BC=10，D为BC的中点．当⊙A半径为6时，则D点与⊙A位置关系为（ ）
| A． | 圆上 | B． | 圆内 | ||
| C． | 圆外 | D． | 以上三种都有可能 |
11．
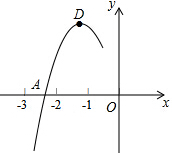抛物线y=ax2+bx+c的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图，则以下结论不正确的是（ ）
抛物线y=ax2+bx+c的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图，则以下结论不正确的是（ ）| A． | b2-4ac＜0 | |
| B． | a+b+c＜0 | |
| C． | c-a=2 | |
| D． | 方程ax2+bx+c-2=0有两个相等的实数根 |