题目内容
6. 如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )
如图,在正方形ABCD中,AB=2,延长AB至点E,使得BE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{11}{4}$ | D. | $\frac{\sqrt{26}}{2}$ |
分析 连接AC,易得△ACF是直角三角形,再根据直角三角形的性质即可得出结论.
解答 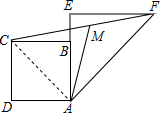 解:连接AC,
解:连接AC,
∴四边形ABCD是正方形,
∴∠BAC=45°.
∵EF⊥AE,EF=AE,
∴△AEF是等腰直角三角形,
∴∠EAF=45°,
∴∠CAF=90°.
∵AB=BC=2,
∴AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
∵AE=EF=AB+BE=2+1=3,
∴AF=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴CF=$\sqrt{{AC}^{2}+{AF}^{2}}$=$\sqrt{{(2\sqrt{2})}^{2}+{(3\sqrt{2})}^{2}}$=$\sqrt{26}$.
∵M为CF的中点,
∴AM=$\frac{1}{2}$CF=$\frac{\sqrt{26}}{2}$.
故选D.
点评 本题考查的是正方形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
16.2的绝对值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
17.-2016的倒数是( )
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
1. 如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )
如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )
 如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )
如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )| A. | abc>0 | B. | 当x<1时,y随x的增大而增大 | ||
| C. | a+b+c>0 | D. | 方程ax2+bx+c=0的根为x1=-3,x2=5 |
11.在平面直角坐标系中,下列函数的图象经过原点的是( )
| A. | y=-2x+1 | B. | y=-2x | C. | y=-$\frac{2}{x}$ | D. | y=-x2+1 |
18. 一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )
一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )
 一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )
一次函数y=(m+1)x+2在平面直角坐标系中的图象如图所示,则m的取值范围是( )| A. | m>-1 | B. | m<-1 | C. | m≥-1 | D. | m≤-1 |
15.一个几何体的主视图和左视图都是边长为2cm的正三角形,俯视图是一个圆,那么这个几何体的侧面积是( )
| A. | πcm2 | B. | $\sqrt{3}$πcm2 | C. | 2πcm2 | D. | 4πcm2 |
 在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,则△ABC的面积为30.
在△ABC中,中线AD、BE相交于点O,若△BOD的面积等于5,则△ABC的面积为30.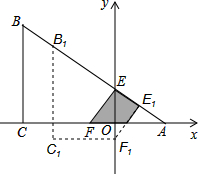 如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.
如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.