题目内容
11.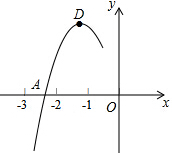 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )| A. | b2-4ac<0 | |
| B. | a+b+c<0 | |
| C. | c-a=2 | |
| D. | 方程ax2+bx+c-2=0有两个相等的实数根 |
分析 由抛物线与x轴有两个交点得到b2-4ac>0;有抛物线顶点坐标得到抛物线的对称轴为直线x=-1,则根据抛物线的对称性得抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,所以当x=1时,y<0,则a+b+c<0;由抛物线的顶点为D(-1,2)得a-b+c=2,由抛物线的对称轴为直线x=-$\frac{b}{2a}$=-1得b=2a,所以c-a=2;根据二次函数的最大值问题,当x=-1时,二次函数有最大值为2,即只有x=-1时,ax2+bx+c=2,所以说方程ax2+bx+c-2=0有两个相等的实数根.
解答 解:∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以A错误;
∵顶点为D(-1,2),
∴抛物线的对称轴为直线x=-1,
∵抛物线与x轴的一个交点A在点(-3,0)和(-2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,所以B正确;
∵抛物线的顶点为D(-1,2),
∴a-b+c=2,
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=-1,
∴b=2a,
∴a-2a+c=2,即c-a=2,所以C正确;
∵当x=-1时,二次函数有最大值为2,
即只有x=-1时,ax2+bx+c=2,
∴方程ax2+bx+c-2=0有两个相等的实数根,所以D正确.
故选A.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )
如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )
 如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )
如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )| A. | abc>0 | B. | 当x<1时,y随x的增大而增大 | ||
| C. | a+b+c>0 | D. | 方程ax2+bx+c=0的根为x1=-3,x2=5 |
19.如图,其左视图是矩形的几何体是( )
| A. |  | B. |  | C. |  | D. |  |
6. 如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )
如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )
 如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )
如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )| A. | 12π-$\frac{9\sqrt{3}}{2}$ | B. | 4π-$\frac{9\sqrt{3}}{2}$ | C. | 12π-9$\sqrt{3}$ | D. | 4π-9$\sqrt{3}$ |
3.下列各图不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在⊙O中,点A为$\widehat{BC}$的中点,若∠BAC=140°,则∠OBA的度数为70°.
如图,在⊙O中,点A为$\widehat{BC}$的中点,若∠BAC=140°,则∠OBA的度数为70°.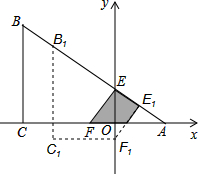 如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.
如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S. 在平面直角坐标系中,已知点A(-1,0),B(-2,2),请在图中画出线段AB,并画出线段AB绕点O逆时针旋转90°后的图形.
在平面直角坐标系中,已知点A(-1,0),B(-2,2),请在图中画出线段AB,并画出线段AB绕点O逆时针旋转90°后的图形. 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )